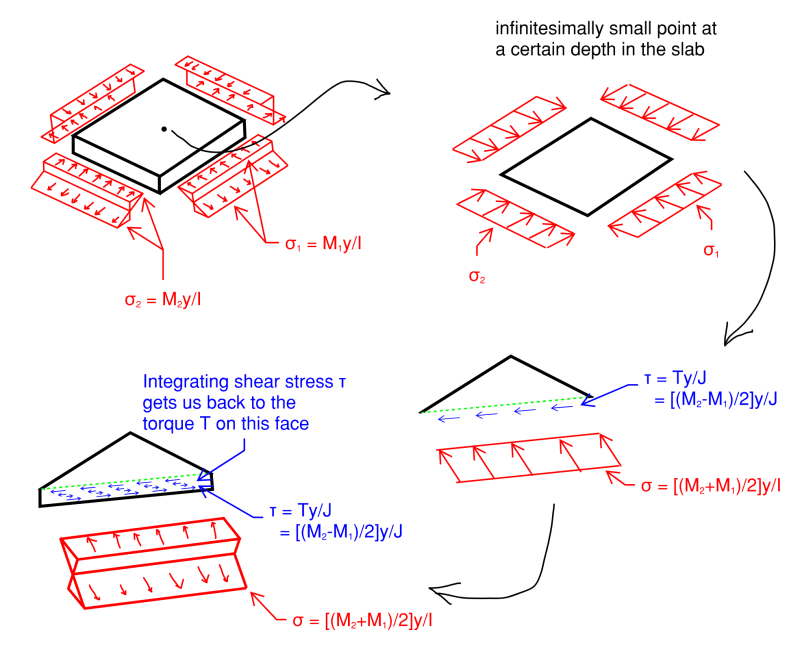
This is more of a theoretical question, which I hope has a simple answer. Please refer to my sketch below.
Does the Mohr's circle concept extent to bending and torsion for a plate?
For example, if we consider a plate subject to principal bending moments of M1 and M2, is it the case that there will always be a maximum torque of (M2 - M1)/2 acting on a plane oriented 45 degrees to the axes of the principal moments?
Then, for the case of M1 = M2, would we expect there to be no torsion acting on any plane?
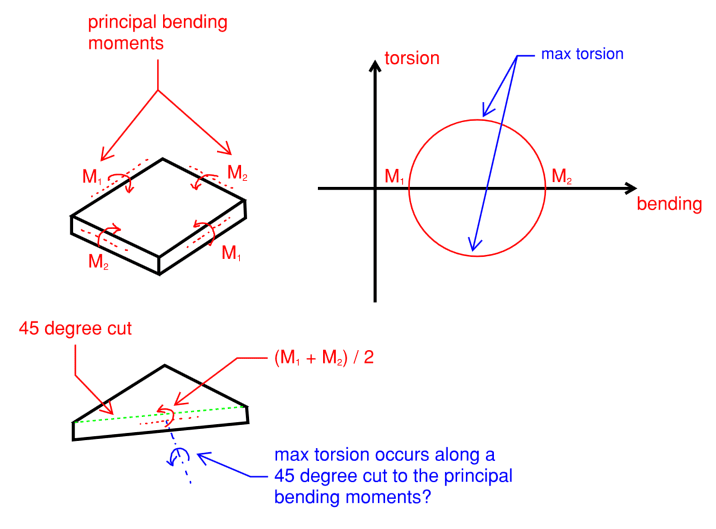
Does the Mohr's circle concept extent to bending and torsion for a plate?
For example, if we consider a plate subject to principal bending moments of M1 and M2, is it the case that there will always be a maximum torque of (M2 - M1)/2 acting on a plane oriented 45 degrees to the axes of the principal moments?
Then, for the case of M1 = M2, would we expect there to be no torsion acting on any plane?