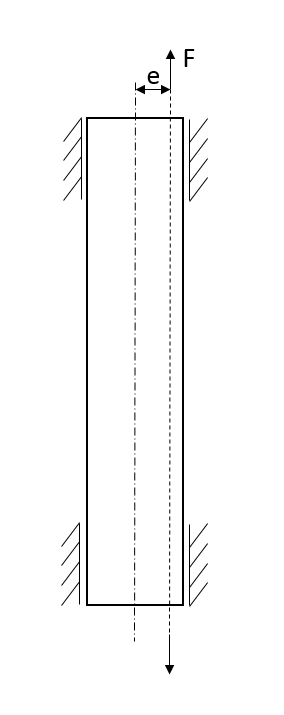
Eccentrically loaded beam moment distribution

[Chris10B]

Hello all,

So, I am familiar with the derivation of the maximum moment and stress of an eccentrically loaded beam with pinned ends. However how does the calculation change when both ends are fixed? Is such a beam overdetermined?

Thanks for your input!

 

[rb1957]

if fixed at both ends then the "beam" is unloaded.

how does the beam interact with the rest of the world ? You show (carefully) no contact at the ends. Say there's a shear connection at the bottom end, then this'll react the beam axial load and the beam will "cock" in the clearances and develop a lateral couple to react the offset load. If the shear attmt is inline with the load then no moment to "the rest of the world", but there'll be an internal moment in the beam.

clear as mud ?

another day in paradise, or is paradise one day closer ?

 

[JAE]

What is this beam/column doing in its application? How do you achieve this pure rotational fixity and pure lateral fixity at the same time as vertical slip?

Check out Eng-Tips Forum's Policies here:
faq731-376

 

[BAretired]

If the ends are fully fixed, the beam does not feel the effect of the force F, i.e. the beam has no stress and no deformation.

If one end of the beam is fixed against rotation but free to move in an axial direction and the other end is fully fixed, the beam feels an axial stress of F/A but no bending.

What is the meaning of "overdetermined"?

BA

 

[MotorCity]

I think the OP needs to clarify the end conditions and load application. To me it appears as if there are "guides" at each end and each side of the member. Graphically, it does not look like there is any end restraint.

 

[rb1957]

"overdetermined" = reduntant, indeterminate

another day in paradise, or is paradise one day closer ?

 

[BAretired]

Well, a beam fixed at both ends against rotation is theoretically indeterminate in the sense that the number of reactions exceeds those determined by statics alone but in this case, it is a trivial indeterminacy because the applied moment is resisted by the fixed ends.

If both end supports permit axial translation, the beam is unstable. The beam needs one reaction to prevent translation. It can be at an end or anywhere along the beam, but it is necessary for stability.

BA

 

[Chris10B]

Re-reading this after myself, I really did not do a good job at explaining the load case!
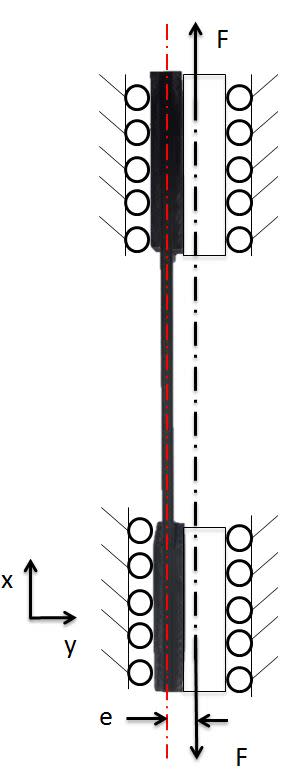
I think the following diagram explains it better.
The case is of an eccentrically loaded tension specimen with the intention of superimposing tension and bending loads.
Fixed supports are actually roller supports, as displacement is allowed in x, but is fixed in y. Under tensile loading the beam center-line (red) should then deflect toward the overall center-line. As a result, there is a bending moment in the beam. What is the distribution of this bending moment along the beam in the x direction?

 

[rb1957]

ok, that's clearer !

there is some moment restraint at each end. Draw a FBD of 1/2 the specimen. In all likelihood the unsupported mid-span of the specimen will deflect towards the load line of action, reducing the off-set moment; this moment will divide itself between the ends and the mid-span.

Depending on what you're trying to test, you could put a hinge at the end of the specimen, then the specimen would be in tension and the off-set moment reacted at the ends (ie a simple tension test). If you remove the rollers, and maybe load on a single point, you'd see the ends rotate as the mid-span tries to unload moment.

another day in paradise, or is paradise one day closer ?

 

[JAE]

I guess if the two ends of the member cannot rotate, there is NO moment in the member. Hook's Law - for internal force to occur in a member, you must have a corresponding deflection.
Since 0 rotation, then 0 moment.

The F x e moment is taken "out" by the boundary condition at that point since you dis-allow rotation in the member at the end.

Check out Eng-Tips Forum's Policies here:
faq731-376

 

[rb1957]

if the end fixity is perfectly rigid then yes, otherwise (in the real world) the two finite stiffnesses (the end fixity and the specimen) will share the moment.

another day in paradise, or is paradise one day closer ?

 

[BAretired]

You should fix one end in x and leave the other end free. Otherwise you have an instability in the x direction. Then you have pure axial tension throughout the beam.

BA

 

[rb1957]

I suspect that the load is applied at one end against a reaction at the other (as i think you're suggesting). I doubt he's got active loading at both ends.

another day in paradise, or is paradise one day closer ?

 

[BAretired]

I suspect you are correct rb1957, but his diagram does not show that. If he were to enter his support conditions into a frame analysis program, he would get an input error.

BA