Hello
I managed to calculate resultant shear force acting on P1, which is caused by the far end force, 250lbs. (P1 has the highest shear force), thanks to the link below.
and it is 505 lbf.
but I have trouble finding shear force acting on the bolts, due to the force on the right most side, close to the bolts)
Would anyone please help me with this calculation?
Thank you
Eccentrically loaded bolted joint
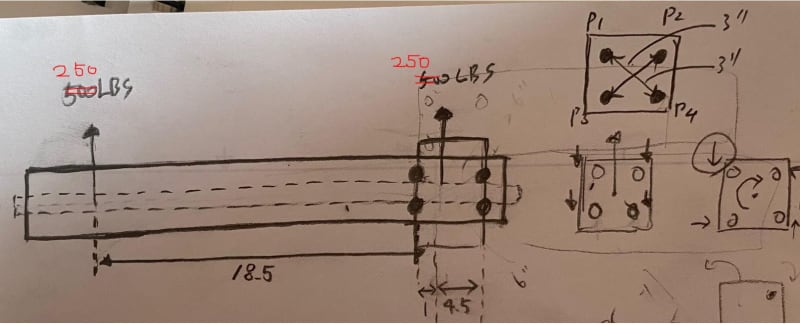
I managed to calculate resultant shear force acting on P1, which is caused by the far end force, 250lbs. (P1 has the highest shear force), thanks to the link below.
and it is 505 lbf.
but I have trouble finding shear force acting on the bolts, due to the force on the right most side, close to the bolts)
Would anyone please help me with this calculation?
Thank you
Eccentrically loaded bolted joint