Effect of foundation width of shear based bearing capacity

[DMI.BE]

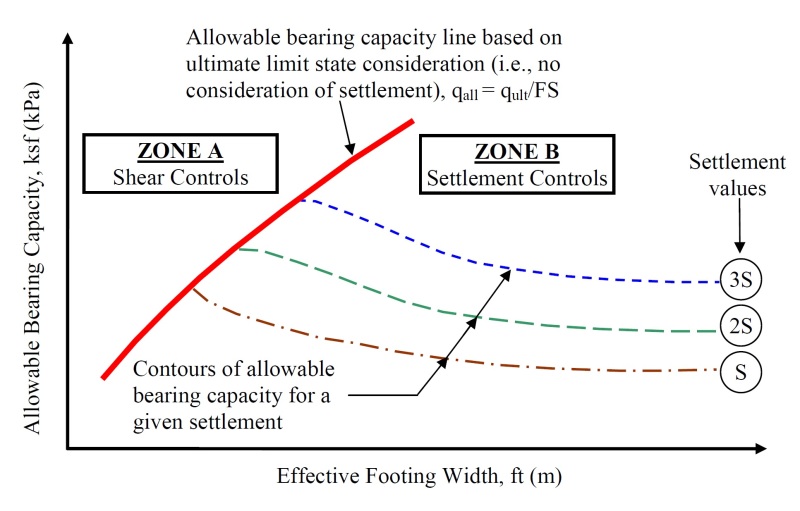
As a general concept explained in geotechnical engineering textbooks, shear based bearing capacity is explained to be increasing with foundation width. Since the 'width' component in Terzaghi's Bearing capacity equation increases, hence is the corresponding increase in ultimate bearing capacity in shear. Physical understanding of this phenomenon is also simple that with increase in foundation width length of failure path increases; longer failure path offers greater resistance to failure (i.e., 'unit resistance' multiplied by 'length of failure path' would be larger). A typical figure is shown in the attachment.

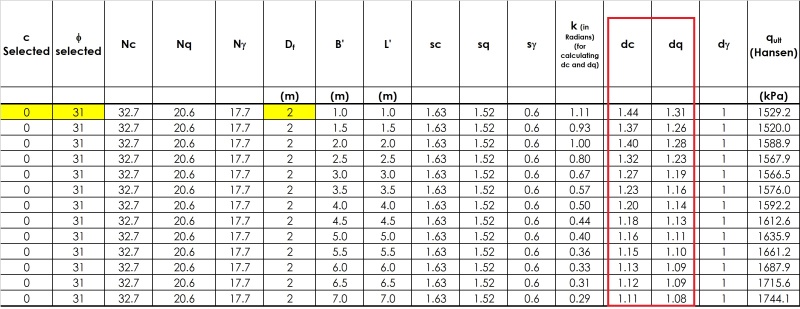
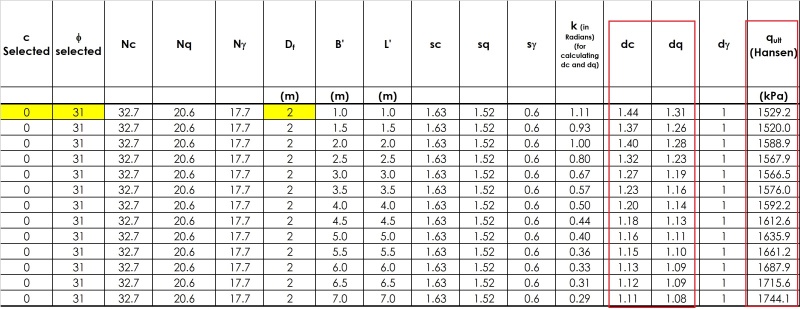
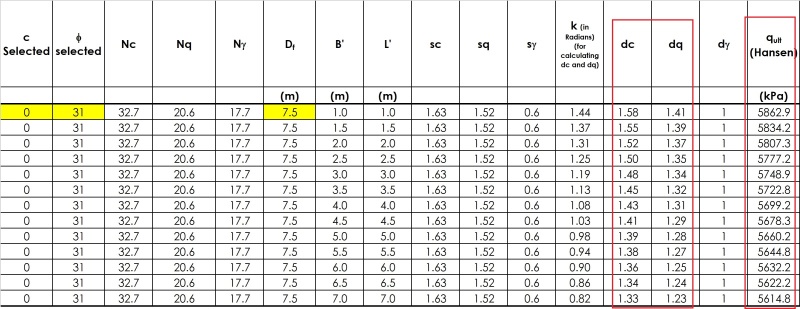
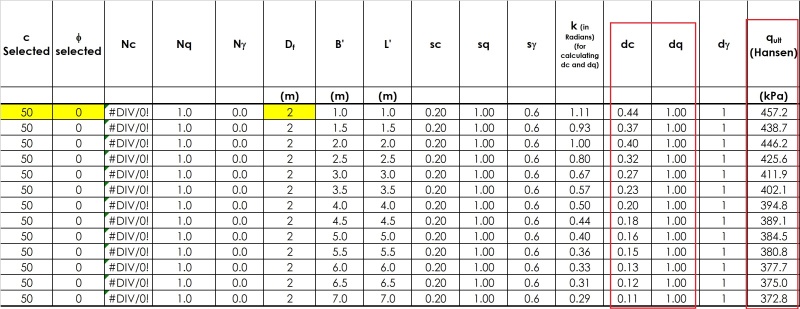
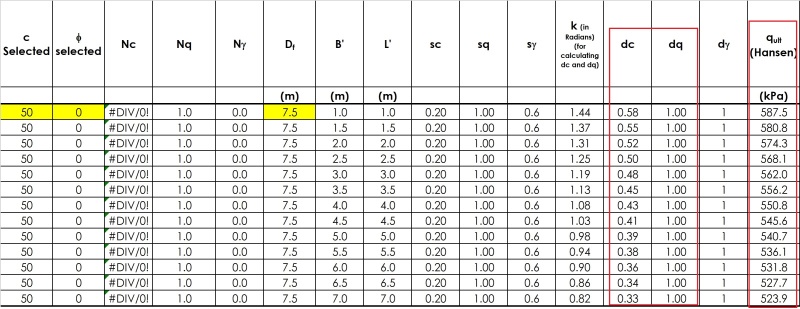
The use of Mayerhof or Hansen bearing capacity equations (i.e., by incorporating shape, depth, inclination factors, etc.) however, gives result which are opposite to the trend explained in previous passage. By using Mayerhof or Hansen factors ultimate bearing capacity appears to decrease with foundation width. A close look into the data show that main reason for this decrease are the values of depth factors 'dc' and 'dq' which decrease with foundation width. I have been searching for a physical explanation of this decrease in ultimate bearing capacity with foundation width, but could not find any. I have even gone through original papers Mayerhof (1963) and Hansen (1970) but they are also silent in this regard. Any valuable input in this regard is appreciated.

 

[oldestguy]

Go to the next post down, by
LeonhardEuler (Structural

Look at my post and the reference by Hough.

 

[DMI.BE]

@oldestguy: Thanks for your comment. I have gone through your comment on the other thread but the discussion there is different than what I want to know. I am simply interested in knowing the physical explanation of decrease in SHEAR based bearing capacity with foundation width, as obtained through Mayerhof or Hansen bearing capacity equations.

 

[LeonhardEuler]

OPcan you include the part of the equation that decreases with foundation width. I am looking at the general bearing equation formulas and the Meyerhoff shape factors and it appears to me that the shape factors increase with an increase in width and of course B is in the numerator of the general bearing capacity equation given in Bowles, Brajas, and Coduto.

 

[DMI.BE]

@LeonhardEuler: See the excerpt from Bowles below where the concerned expressions have been highlighted.

If we keep the depth fixed and increase the width, these factors appear to keep on decreasing since D/B ratio would decrease (see sample calculations in the image below).

 

[DMI.BE]

In an attempt to find a pattern here, I have made a few more trials for which the results are shared here.

Trial-1
Sand
phi=31
c=0
Df=2m
Result: Qult (more or less) increases with foundation width

Trial-2
Sand
phi=31
c=0
Df=7.5m
Result: Qult decreases with foundation width

Trial-3
Clay
phi=0
c=50kPa
Df=2m
Result: Qult decreases with foundation width

Trial-4
Clay
phi=0
c=50kPa
Df=7.5m
Result: Qult decreases with foundation width

So a conclusion I have reached from the above trials is that,
- Qult for sands decreases with width as long as D/B>1, and for D/B<=1, it increases with width.
- Qult for clays decreases with width irrespective of D/B ratio.

 

[LRJ]

Seems like a flaw in the method, to me.

Nonetheless, it's important to remember that, while the stress is decreasing, the overall load that can be taken is increasing considerably (force = stress * area).

 

[LeonhardEuler]

I wouldn't say the numbers are decreasing, because in the depth factor equation it is a 1+D/B so you'll never have that factor dip below 1.0. I'm not sure the reason that an increased width decreases the benefit of a deeper foundation, but I would like to know. Perhaps you can track down a derivation of Meyerhoff's equations.

As an idea I wonder if it has anything to do with the concept that the foundation "recruits" an area of soil outside of its planar boundary. what I have seen is roughly an additional 2 feet on each side. This number is essentially fixed and doesn't vary with foundation width. In that way the percentage of additional soil recruited for bearing capacity is greater for a more narrow foundation than it is for a wider one. I have no reference to back this up, but maybe its good for thought and others can weigh in.

 

[Okiryu]

DMI.BE, that is a nice observation. Thanks for sharing it with us. I has been thinking that the bearing capacity increases with the size of the footing. Perhaps, most of the people does not note this because for most of the times, foundation design is based on settlement considerations.

Anyway, I think that one of the reasons for the bearing capacity to decrease when using the Depth Factors is because the effective angle of friction reduces with depth (increasing of confining stress). For example, look at the non-linear hyperbolic soil model from Duncan and Chang. Since the bearing capacity factors depend on the friction angle, perhaps this was taken into the account. Appears that Brinch Hansen depth factors and the hyperbolic model by Duncan and Chang were published in the same year (1970) so perhaps Brinch Hansen considered the hyperbolic model when he developed the depth factors.

I was looking at my school notes and recalled that increasing the depth or effective confining pressure suppresses the dilation that occurs. So at high effective confining pressures, all that is measured is the sliding friction (constant volume shear strength). As the effective confining pressure decreases, the tendency for dilation (particles "climbing over one another") increases. Note that the effective friction angle is the sum of the sliding friction angle plus the dilation angle.

 

[geov86]

DMI.BE this is an interesting observation indeed. The phenomenon to which are referring here we geotechnical engineers call it "scale effect" and it is exactly the reduction of ultimate bearing capacity with the increase in foundation width. It is oftentimes the cause of underestimations regarding the bearing capacity.

In fact, three possible reasons (as far as I can recall) were believed to be responsible for this: reduction in φ due to increased stress, difference in φ among locations exerted on slip bands along with the progress of failure, and impacts of the ratio of sand particles to foundation width. However, so far we don't know how much each of the above factors affects bearing capacity

 

[DMI.BE]

@Okiryu: Thanks for pointing attention towards the decrease in friction angle with increasing stress. However, I don't this that this effect is significant enough compared to the overall decrease in bearing capacity. Further, I skimmed through the original paper by Hansen, and it does not mention any reference towards Duncan and Chang. Probably, without the computing powers of today, this possibility was overlooked during original derivation.

 

[DMI.BE]

@geov86: Thanks for sharing your point, but I believe scale effect would not affect these value because the size of the footing is already considerably large compared to the soil particles. Such phenomenon is more prominent when dealing with small scale prototypes during physical modelling of geotechnical engineering problems.