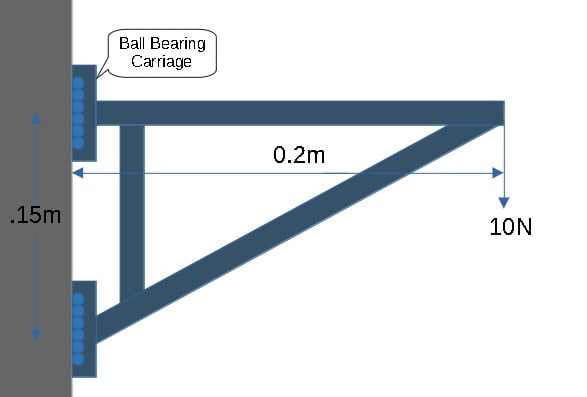
I got question on what is happening to the moment and forces on a ball bearing carriage with a lever arm. Basically the carriage is at rest and is moving/accelerating up and there's a load of 1kg at the end of the lever 0.2m from the carriage.
If it was not moving, the moment about the carriage is 1kg*0.2m=0.2kg*m (static problem), but once the carriage accelerates let's say 2G (gravitation force). I assume moment about the carriage will increase. So can someone explain what is happening once it starts moving and can the moment still be solved if we know the force used to move the carriage, in this case 2G?
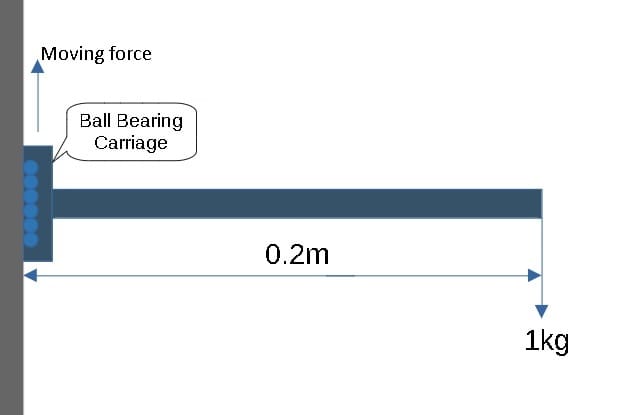
If it was not moving, the moment about the carriage is 1kg*0.2m=0.2kg*m (static problem), but once the carriage accelerates let's say 2G (gravitation force). I assume moment about the carriage will increase. So can someone explain what is happening once it starts moving and can the moment still be solved if we know the force used to move the carriage, in this case 2G?