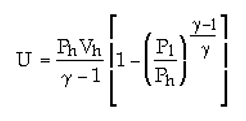Ameen1985
Mechanical
- Feb 10, 2021
- 17
Hello all,
For a vessel with a constant volume of 8 m^3 with a 15 bar pressurized air in it. What is the contained energy in the vessel?? If the pressure changes from 15 bar to 7 bar or to 20 bar; how much energy does the vessel lose or gain ? Assuming isentropic processes with n or k = 1.4
I found in the literature different equations to solve such a problem. It I think it should be easier than that. Many thanks in advance.
As you can see three different equations with different answers.


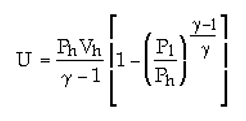
For a vessel with a constant volume of 8 m^3 with a 15 bar pressurized air in it. What is the contained energy in the vessel?? If the pressure changes from 15 bar to 7 bar or to 20 bar; how much energy does the vessel lose or gain ? Assuming isentropic processes with n or k = 1.4
I found in the literature different equations to solve such a problem. It I think it should be easier than that. Many thanks in advance.
As you can see three different equations with different answers.