compe_ad
Civil/Environmental
- Apr 20, 2022
- 71
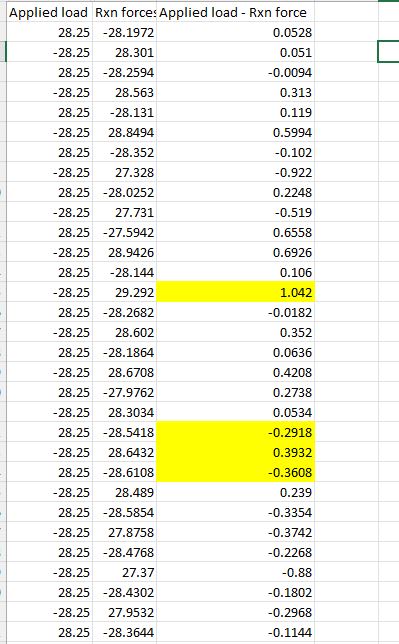
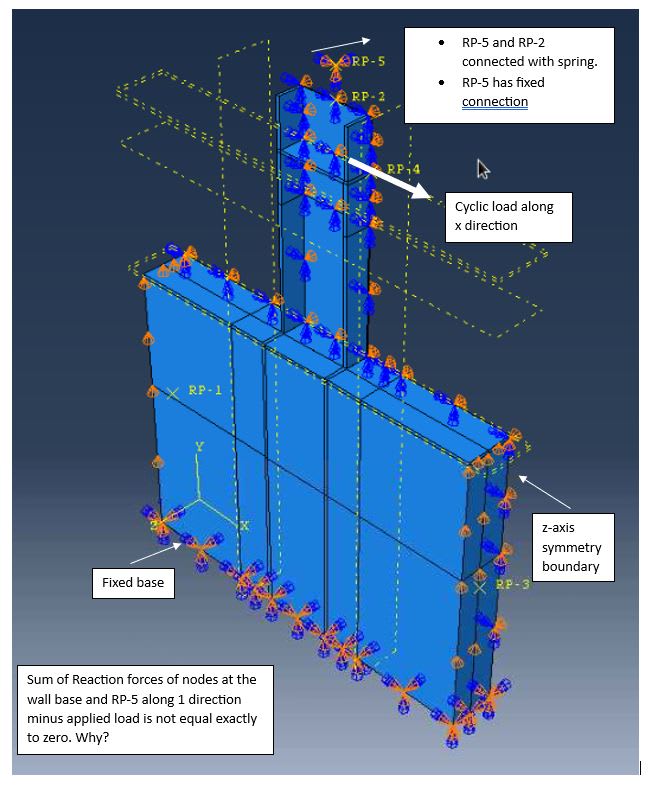
Hi all! I am checking the equilibrium of forces along the applied load direction for my Abaqus model. The forces are not exactly in equilibrium. Please look at the picture and table attached. It is a Abaqus explicit analysis. Am I missing something while checking the equilibrium.