Equivalent Nodal forces of a multiple loaded beam?

[PPoyyyy]

So i have to do the stair analysis by hand , And i couldn't find the equivalent nodal forces on the inclined beam

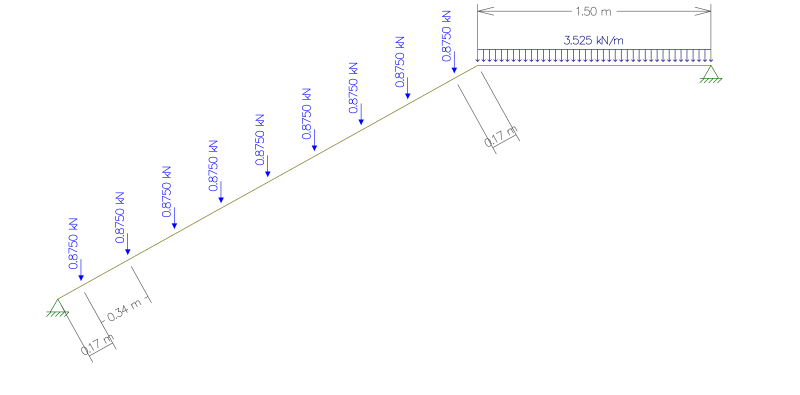
Is there a way to do that without cutting the beam to several parts?
If not, Is there a way to turn the point loads into uniformly distributed?
Edit: What i want is to find the reactions so i can do a Buckling analysis on the inclined member and design the transversal beam that holds them.

 

[JAE]

For that layout I would suggest your point loads divided by the point load spacing = an equivalent uniform load.

Check out Eng-Tips Forum's Policies here:
faq731-376

 

[rb1957]

do you mean you want to transform the inclined forces to their normal and parallel components ?

how to replace an array of uniformly pitched forces with an equivalent distributed load ... nP/L ?

another day in paradise, or is paradise one day closer ?

 

[klaus.]

What do you want to do ?????
Design the stair beam ?
Calculate the forces in the beam ( Moment Shear .... )
Calculate deflections.....

For a hand analysis it is usually easier using single point loads rather than distributed line loads




best regards
Klaus

 

[PPoyyyy]

What i want is to find the reactions so i can do a Buckling analysis on the inclined member and design the transversal beam that holds them.

 

[klaus.]

Buckling should be no problem ( what type of material ?? )

Are both supports fixed horizontally ??
if not then the system is statically determined and you can calculate support forces very easy by hand



best regards
Klaus

 

[PPoyyyy]

Yeah i kinda figured that would be the case..But i have to check for it , Material is Steel and both members are Pinned.
Now that i think about it what should be the other support on the inclined beam if i wanted to isolate it for buckling check?.
Thank all for the help Guys

 

[txeng91]

You could convert the point loads on the sloping part to an equivalent uniform load as JAE said and calculate moment and deflection using standard formulas (wl^2/8 for moment and 5wl^4/384EI for deflection) and I think that would work assuming the stringer and landing beam are the same member. I typically like to use a roller at the end of a stringer to avoid counting on it for axial load but if you have adequate rigid horizontal connections at each end I don't see any reason you couldn't factor that into your analysis to give you some extra capacity. In any case, I would make sure you have an adequate moment connection at the kink.