alphanumericname
Structural
Hello,
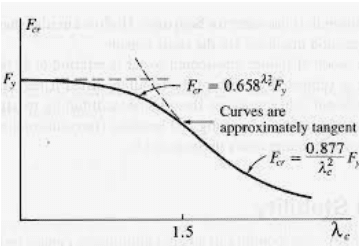
Does Euler's Formula for buckling generally give a good, quick estimate of the critical buckling load, or should it be disregarded in exchange for modern buckling formulas provided by AISC or ACI? I am studying for my PE and am trying to decide whether or not it can be used as a time saver when solving multiple-choice problems.
Thanks.
Does Euler's Formula for buckling generally give a good, quick estimate of the critical buckling load, or should it be disregarded in exchange for modern buckling formulas provided by AISC or ACI? I am studying for my PE and am trying to decide whether or not it can be used as a time saver when solving multiple-choice problems.
Thanks.