EUROCODE LONG TERM DEFLECTION 1

[PSR_1]

EN 1992 section 7.4.1(4) states :

"The appearance and general utility of the structure could be impaired when the calculated sag of a beam, slab or cantilever subjected to quasi-permanent loads exceeds span/250. The sag is assessed relative to the supports. Pre-camber may be used to compensate for some or all of the deflection but any upward deflection incorporated in the formwork should not generally exceed span/250".

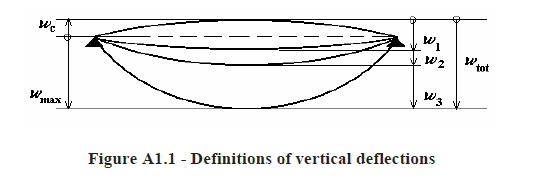
The code clearly states that span/250 limit should be compared against deflection due to quasi-permanent loads( including the effect of creep and shrinkage of course) and figure A1.1 of EN 1990(see the attachment) shows some detail of deflection considered in Eurocode. I am confused in what way to stablish long term deflection check using Eurocode.

 

[HTURKAK]

Is this the figure that you want to post?

 

[PSR_1]

That is correct HTURKAK.

 

[HTURKAK]

Please be more specific.. If you want to calculate the long term deflection pls look to (7.4.3 Checking deflections by calculation ),
If you want to omit the deflection you should look to the requirements stated (7.4.2 Cases where calculations may be omitted ).

If you have a specific real question, pls share more info. to get specific respond.

 

[hardbutmild]

If you're asking what are w1, w2 and w3 in the figure provided by HTURKAK, then they are the deflection due to permanent loads, deflection due variable load and deflection due to long term change of the deflection.

If you're asking how to calculate the deflection then it seems to me like a very complex problem so I decided to comment. For example, I always wondered should we take cracking under quasipermanent (QP) load or under the characteristic (CH) combination when calculating the deflection. I've always calculated the cracking from CH, then used that stiffness to check the deflection under QP load. My reasoning is the following: In the working life of a structure (50 years) we can expect that a CH will come at least once. It could be a day after construction, or it could be 40 years after construction. But, when it comes it probably won't last long, so it's not a problem if the deflection under CH goes over L/250 (hence, check the deflection for QP). BUT, when the CH came, it cracked the element so that when the load goes back to QP it's stiffness is reduced like under the CH. Therefore, I use CH stiffness, but QP load for the calculation of the deflection. Am I onto something or am I completely off?

 

[HTURKAK]

This is copy and paste from the code

(In most cases it will be acceptable to compute the deflection
twice, assuming the whole member to be in the uncracked and fully cracked condition in turn,
and then interpolate using Expression (7.18).)

You should perform both analysis for fully cracked (Icr ) and Uncracked Section Analysis (Ic)

The deformation is the additive of (the viscous part due to permanent loads , the total deformation ( due to the quasi-permanent part, w2 of variable loads , the elastic deformation due to the remaining part (1 − w2)p″1 of variable loads.).

IMO, It is better to remind (7.16.a) and (7.16.b).

 

[hardbutmild]

I agree that it's better to avoid the check altogether (I also advocate for it), but I don't think that you understood what I was trying to say. Let's presume that the check is needed (if it isn't needed, the problem is trivial). You mention (7.18) and the fact that we should interpolate between the fully cracked and uncracked deflection (that's the factor zeta), but the factor zeta depends on the value of stress (sigma[sub]s[/sub]). Is this stress calculated for quasipermanent or characteristic load? Because I've seen people calculate it for stress at QP with beta factor 0,5 AND for stress at CH with beta factor 1,0. It's not really well defined in the code. The code says "sigma[sub]s[/sub] is the stress in the tension reinforcement calculated on the basis of a cracked section", it's not clear should I calculate two different values of final deflection, one where sigma[sub]s[/sub] is due to CH and one where sigma[sub]s[/sub] is due to QP (because at both QP and CH section is cracked), or just the one for QP? I believe that only QP needs to be checked, but I'm not sure since it's not clear from the code. Also, what to do if sigma[sub]s[/sub] for QP is lower than a cracking stress? Because, if for example a year after construction we have a large load (let's say CH), it will crack a section. Therfore, even though for QP we have sigma[sub]s[/sub] lower than cracking sigma, our section is cracked (because we had a higher load sometime in the history), but (7.18) would say that deflection is the same as uncracked.
Also, what does the beta factor even mean? The code says, beta = 1 for a single short-term loading and 0,5 for sustained loading. When do we need to check a single short term loading? Is it some sort of accidental load or is it standard CH value? And should we also consider creep and shrinkage effects for that loading? Because that single shot term loading could come after 40 years of use.

For example, say that:
cracking stress in steel

sigma[sub]sr[/sub] = 100 MPa​

stress in steel for QP

sigma[sub]s[/sub](QP) = 200 MPa​

stress in steel for CH

sigma[sub]s[/sub](CH) = 300 MPa​

zeta = 1 - beta (sigma_sr / sigma_s )[sup]2[/sup]

zeta(QP) = 1 - 0,5* (100/200)[sup]2[/sup] = 0,88
zeta(CH) = 1 - 1,0* (100/300)[sup]2[/sup] = 0,84

Which one do I use to do the check? (Now, I know 0,84 and 0,88 are close, but this is just an example, they can be more different in real situations.)

I am asking all this because calculating the deflection is very tiresome so I'd like to know if I need to check CH load at all? I am asking you since you seem to know about the subject.

 

[HTURKAK]

I have copied and pasted the definition of β,σs,σsr below;

β is a coefficient taking account of the influence of the duration of the loading
or of repeated loading on the average strain
= 1,0 for a single short-term loading
= 0,5 for sustained loads or many cycles of repeated loading.

-If you are looking for long term deflection; you are expected to use β =0.5 and loading will be Quasi-permanent load (QP) and you shall consider the effect of creep and shrinkage,( (QP) could be taken as the dead load plus 25% of the imposed load for housing bldgs.)

- If you are looking for short term deflection ;you are expected to use β =1.0 and loading will be accidental load or standard CH value and you shall add the effect of creep ( interpolate the long therm effect considered for quasi-permanent load with loading age ) and shrinkage,

σs is the stress in the tension reinforcement calculated on the basis of a
cracked section
σsr is the stress in the tension reinforcement calculated on the basis of a
cracked section under the loading conditions causing first cracking

Alternatively you can use the formula ζ = 1 − β (Mcr/M) 2.

Regarding your calculation ;

zeta(QP) = 1 - 0,5* (100/200)2 = 0,88 is O.K. for QP loading
zeta(CH) = 1 - 1,0* (100/300)2 = 0,84 is O.K. for CH loading .

Does this reply answer your question ? If not, open a separate thread with a real question with real dimensions etc. A few days ago, several people including me, responded to a thread and the thread disappeared ,i think the OP did it with delete option and went a way. Imagine how i am disappointed..

 

[hardbutmild]

Thank you, this answered my question. Although I'm still not sure of one thing, when do I need to check the short term deflection and how to know at what age will it come (to know what creep factor to take)? Is this check used only for some special event (for example if I want to check a bridge for a passing of a special vehicle, because then I'd know both the loading and the time), or is it supposed to be checked always (for example in a standard residential building for characteristic load, because then I don't know at what age should I assume it)? I'd like a thread about deflection calculation since it can be confusing. If I find time, I might open a thread for an in depth discussion about all the details concerning deflection, until then, thank you very much for your help.

 

[Agent666]

I think what 'short term' is referring to is not loading at an early age, it is a higher intensity load applied over a shorter time period. The 'long term' case is more the average load intensity over a longer period on which time dependant cases like creep are based.

Short term is looking at peaks that might occur instantaneously, but would include the appropriate longer term effects that have been determined under the longer term load conditions that have occurred up until the time you are interested in.

Long term is looking at a longer term average load and the effects that causes over time from initial loading up until the time you are interested in.

Evaluate short term case at any time...
For example the short term deflection immediately following construction would have the material properties and any creep/shrinkage included that occur up until that time.
For example the short term deflection at 50 years later would have the material properties and any creep/shrinkage included that occur up until that time.
Does that make sense?

 

[hardbutmild]

Agent666, I agree with you about everything.
If you were replying to me, I don't think I follow though.

Evaluate short term case at any time...

This is what I have trouble with. When do i NEED to check the short term deflections?
EC2 says that deflection check is needed for:
a) aesthetics (this is L/250 for QP and long term load)
b) functioning (this is L/500 for QP after construction. I presume this is also for long-term? It doesn't say, but it makes more sense to me.)

The code doesn't mention short term deflection at all (or am I blind?). It's only mentioned in the beta factor value.
No limits for it, no directions as to when the check is needed for the short term.
In your examples:

For example the short term deflection immediately following construction would have the material properties and any creep/shrinkage included that occur up until that time.

Okay, say I do the short term check for characteristic load combination at that point in time. It's L/400. Is this acceptable? Should I make this check for every structure?

For example the short term deflection at 50 years later would have the material properties and any creep/shrinkage included that occur up until that time.

Okay, say I do the short term check for characteristic load combination at that point in time. It's L/200. Is this acceptable? Should I make this check for every structure?

I also have some problems with the philosophy of deflection calculation, but I'd need to prepare an example to better illustrate it.

 

[HTURKAK]

In general , the accepted criteria is that, a deflection larger than span/250 should be avoided from the appearance point of view.


Damage to non-structural Members (like partition walls),is a consequence of excessive deformation. The common specified limit deflection is span/500, for deflection occurring after construction of the partitions.

It should be assumed that all quasi permanent loading QP starts at the same time.

 

[hardbutmild]

@HTURKAK
That's exactly what I wrote, so I don't understand the point of your comment.
It seems like we have a communications problem, I'll try to sketch a few things and make a new thread with a more general discussion about deflections.

 

[HTURKAK]

May be i could not explain what i want to say ( due to i am not a native English speaker ).

I want to say ;

- a deflection larger than span/250 should be avoided from the appearance point of view. this is long therm deflection with QP loading,

- Damage to non-structural Members (like partition walls),is a consequence of excessive deformation. The common specified limit deflection is span/500, for deflection occurring after construction of the partitions. That is, the initial deflection occuring just after construction of partition walls should be subtracted in order to see the remaining deflection is acceptable or ot for sensitive partition walls..

Pls post a new thread with some real numbers and a sketch so we can discuss in detail..

Regards..