Sajjad2164
Mechanical
- Dec 22, 2015
- 55
Hello
I've performed a linear (eigenvalue) and non-linear buckling problem, and everything went perfect except for a question I couldn't find its answer to. The question was that when you applied a fraction of eigenvalues to your nonlinear buckling analysis, do you know exactly the magnitude of the displacements you applied as the geometry imperfections? To answer the following question, I performed a simple problem (rectangular plate modeled by shell elements) and found its first five eigenvalues. The displacements are somehow scaled. I'm assuming if I multiply the scale factor to the magnitude of the displacements I'd get the exact values of those displacements, and I'd be able to answer the question I was asked! Do you agree with that statement? If anyone can guide me on this issue I'll appreciate it!
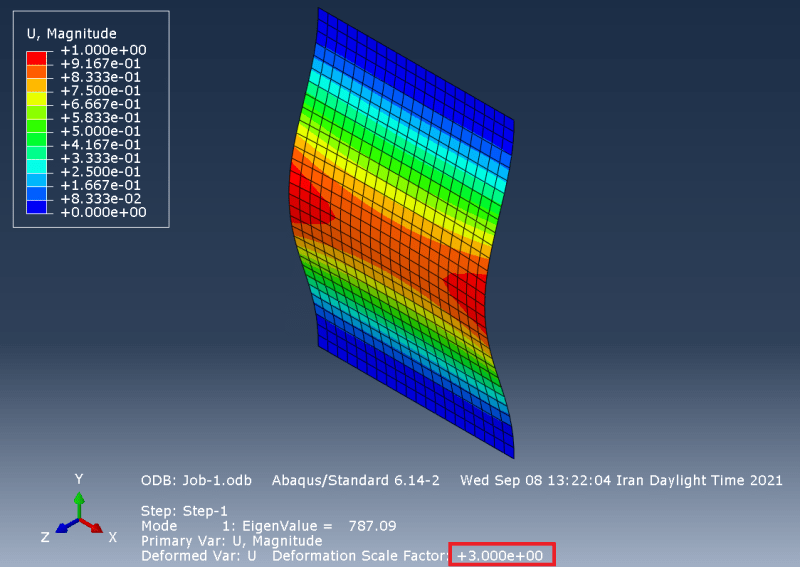
I've performed a linear (eigenvalue) and non-linear buckling problem, and everything went perfect except for a question I couldn't find its answer to. The question was that when you applied a fraction of eigenvalues to your nonlinear buckling analysis, do you know exactly the magnitude of the displacements you applied as the geometry imperfections? To answer the following question, I performed a simple problem (rectangular plate modeled by shell elements) and found its first five eigenvalues. The displacements are somehow scaled. I'm assuming if I multiply the scale factor to the magnitude of the displacements I'd get the exact values of those displacements, and I'd be able to answer the question I was asked! Do you agree with that statement? If anyone can guide me on this issue I'll appreciate it!

