waIkman
Mechanical
- Apr 21, 2021
- 8
Hello everyone,
I am having trouble with PSD curves, it's clearly not my cup of tea and maybe someone can help me on this.
I have 2 different vibration cases that I'd like to compare, given as follows:
1- Acceleration 45m/s^2 / displacement 19mm / Frequency 11Hz -> To me this is a simple sine wave.
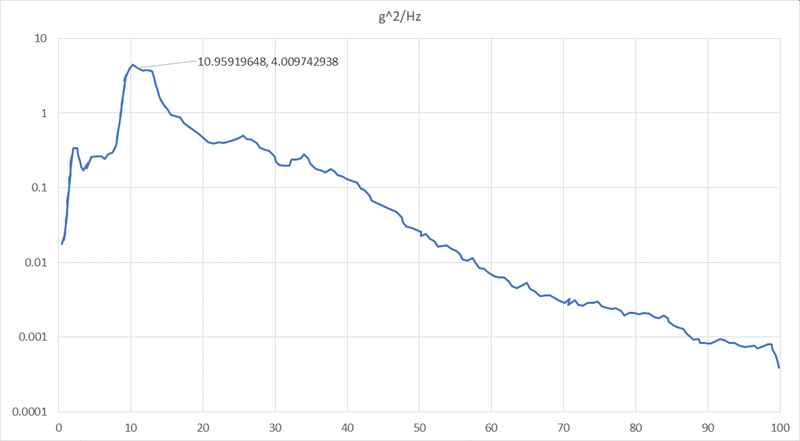
2-
note: the x values are in Hz
I don't really know what I can extract from that PSD to compare it to the first case. I've heard that I should use Mile's equation to extract an acceleration value at a given frequency, but I thought this was correct at resonant frequencies and when we know the damping factor which I don't.
In the best world I'd like to know if the acceleration at 11Hz in the n°2 case is lower or higher than the one in the first case.
Thank you in advance for any help,
Have a great day.
I am having trouble with PSD curves, it's clearly not my cup of tea and maybe someone can help me on this.
I have 2 different vibration cases that I'd like to compare, given as follows:
1- Acceleration 45m/s^2 / displacement 19mm / Frequency 11Hz -> To me this is a simple sine wave.
2-

note: the x values are in Hz
I don't really know what I can extract from that PSD to compare it to the first case. I've heard that I should use Mile's equation to extract an acceleration value at a given frequency, but I thought this was correct at resonant frequencies and when we know the damping factor which I don't.
In the best world I'd like to know if the acceleration at 11Hz in the n°2 case is lower or higher than the one in the first case.
Thank you in advance for any help,
Have a great day.