FFT real amplitude value 2

[Luis Freire]

Hello,

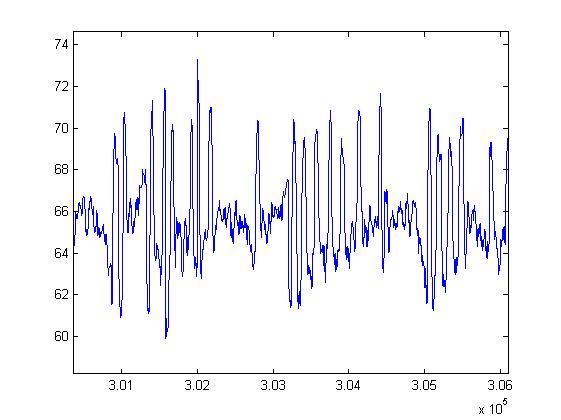
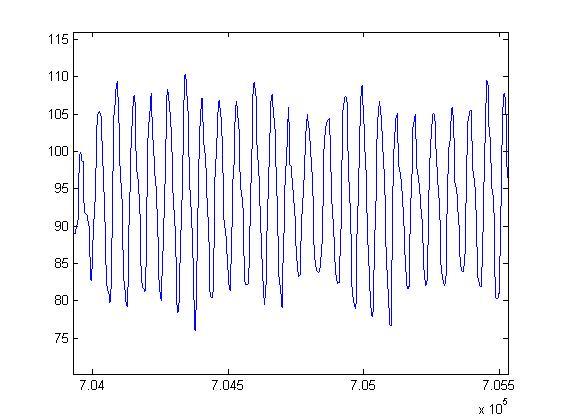
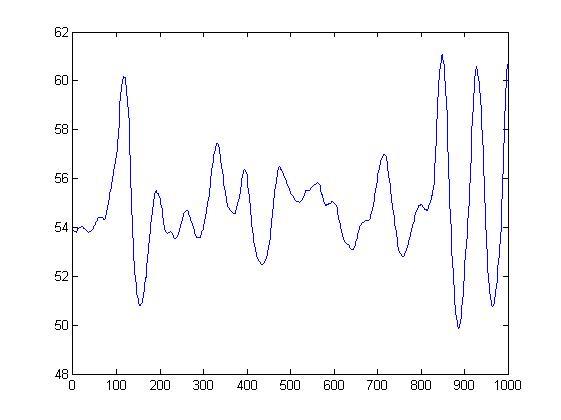
I want to implement the fast fourier transformation on an aperiodic signal, which you can see in the next picture:

The first question came here, can I use the FFT in an aperiodic singnal?
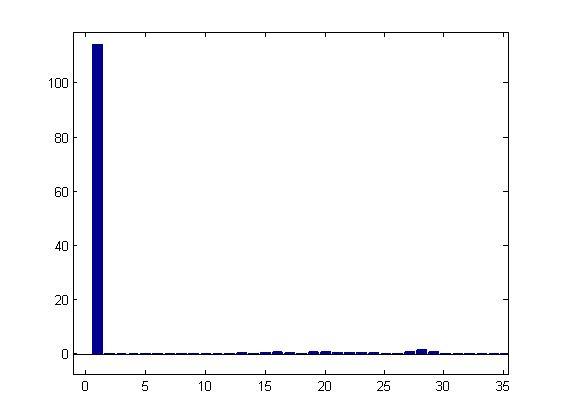
Once I execute the matlab code I obtain the output of the transformation, which you cant see in the next picture:

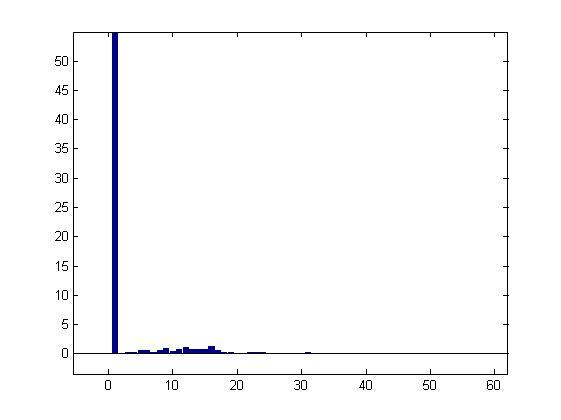
As you can see, the first value (DC offset) is correct and it corresponds with the offset of the signal, but the remaining values of the amplitude of the FFT does not corresponf with the real values of the amplitude of the signal, and the FFT notmalization is done. Why this colud be possible?

Thank you!

 

[IRstuff]

?? FFT amplitude is the amplitude of the individual frequency, which you cannot see in the time series.

Moreover, because it's aperiodic, you probably used a window to kill the aliasing . The FFT implicitly calculates as if your signal were periodic relative to your window, which may result in aliasing and other deleterious effects.

TTFN (ta ta for now)
I can do absolutely anything. I'm an expert!

https://www.youtube.com/watch?v=BKorP55Aqvg

faq731-376 forum1529 Entire Forum list

http://www.eng-tips.com/forumlist.cfm

 

[hacksaw]

subtract the constant term in your FFT data and replot,
your amplitudes are fine,

 

[Luis Freire]

I think that there are not fine, look at the real amplitudes there is one in the range of 5 and that is not represent in the FFT amplitude values.

 

[btrueblood]

You realize the amplitudes sum at some points in time, and subtract at other points in time?

 

[hacksaw]

When you seek the spectral content of your data, the constant (or average dc term) is of secondary importance, so you remove it from the figure. What's left is the amplitude spectra absent the dc term.

As one of the earlier responders has suggested, windowing is encouraged, to avoid mis-representing the actual data stream.

Without a proper window, you have basically assumed that your data repeats itself indefinitely. There are a number of excellent texts covering the matter.

 

[IRstuff]

FFT -- Fast Fourier Transform -- transform a time-domain signal into a frequency domain "signal;" essentially, your "real" (time-domain) signal is assumed to be constructed from a Fourier series with arbitrary phases.

Unless there is a single dominant frequency, each point of the "real" signal will be a sum of contributions of every wavelength in your FFT. In many cases, you need to run short-term FFTs or Wigner transforms if the frequencies or their amplitudes are not constant over time.

TTFN (ta ta for now)
I can do absolutely anything. I'm an expert!

https://www.youtube.com/watch?v=BKorP55Aqvg

faq731-376 forum1529 Entire Forum list

http://www.eng-tips.com/forumlist.cfm

 

[Luis Freire]

I think that both of you are correct encouraging me to use a window function to reduce the spectral leackage, but I understand that the window function depends on the frecuencies and the amplitudes that you have in your data. Have a look at the next pictures that represent two different periods of my signal. If you see them more in detail, you can notice that they have different frecuencies and also different amplitudes within the same frecuency.

That pictures represent only two of the vast amount of periods I have, so I understand that I have to use a different window function for each and also a different resolution (fs/N) for each to catch the real amplitude of the frecuencies I want.

 

[hacksaw]

Luis,

You are currently using the default FFT windowing, that presumes that your data set automatically repeats itself with a period equal to the time interval of the data.

The term "windowing" refers to various means for tapering off the time series to avoid "leakage effects" or frequency content that does not represent your data.

There are a half-dozen "windows" to choose from, if the data is semi-periodic common to fluid movement, Hilbert-Huang transforms are commonly used, but that in itself is anouther topic.

 

[Luis Freire]

So I have to "window" my signal as you can see in the picture, you can also notice that I remove the offset of the signal.

And now I implement again the FFT with this signal, and this is the output.

It still doesn't represent the real value of the amplitude, any idea?

 

[Luis Freire]

Sorry I used the Hamming windowing function:
w=0.5-0.5*cos(2*pi*n/N)

 

[hacksaw]

Luis,

What does your autocorrelation look like?

 

[hacksaw]

Luis,

Interesting that the n=1 component has the magnitude of roughly twice your dc average...

the autocorrelation should show the dc component clearly.

 

[IRstuff]

Are you sure that's your DC component? Why doesn't it plot exactly at the 0 of your graph?

Perhaps you should post some of your data.

TTFN (ta ta for now)
I can do absolutely anything. I'm an expert!

https://www.youtube.com/watch?v=BKorP55Aqvg

faq731-376 forum1529 Entire Forum list

http://www.eng-tips.com/forumlist.cfm