ak82guba
Student
- Oct 15, 2020
- 1
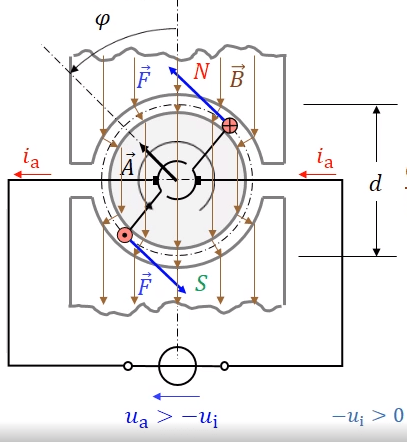
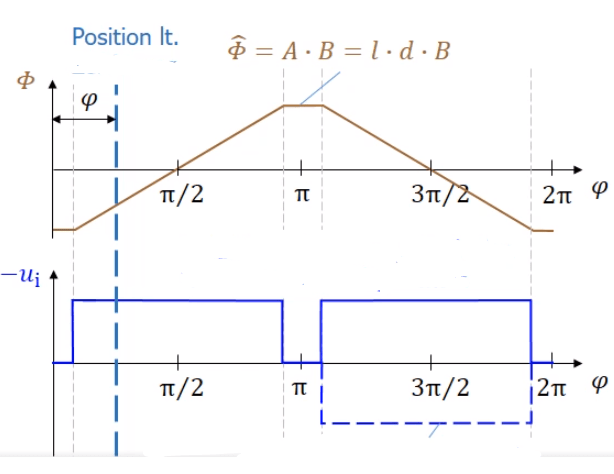
Here are the graphs of flux vs angle and EMF vs angle.
From it, I have to derive the following relation (expected answer) between EMF -Ui and change in flux with respect to time.
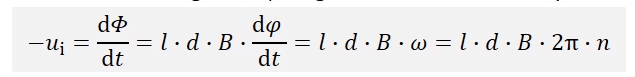
My approach:
I find the function for every piecewise continuous graph which gives me the following result:
Φ=-B∙A,
Φ=((2B∙A)/(π-2θ))∙(φ-π/2),
Φ=B∙A, Φ=-((2B∙A)/(π-2θ))∙(φ-3π/2),
Φ=-B∙A
and lets me find the derivative of flux with respect to angle first which gives me:
dΦ/dϕ=(2B∙A)/(π-2θ),
dΦ/dϕ=-(2B∙A)/(π-2θ)
for two slopes and derivative of flux with respect to time comes out to be:
Ui= (dΦ/dϕ)∙(dϕ/dt)=((2B∙A)/(π-2θ))∙dϕ/dt,
Ui=(dΦ/dϕ)∙(dϕ/dt)=-((2B∙A)/(π-2θ))∙dϕ/dt,
where dϕ/dt=2πn.
It still isn't equal to the answer that I should be getting.
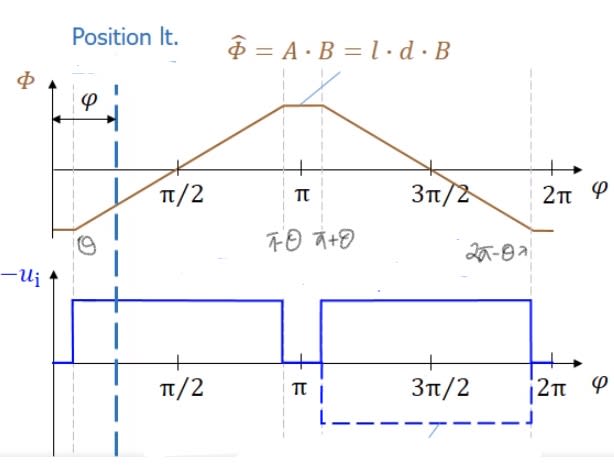
'The commutator gap can be neglected.' does that mean there will be no flat top and bottom on the graph of flux vs angular position? The graph sort of becomes triangular and even in that case where the theta goes to zero, the required answer is not in sight. I need insight on it.
