LeonhardEuler
Structural
Hello,
Is there an easy way to find a deflection diagram from a moment diagram such as what is given in Risa.
I am attempting now and this is what I have come up with.
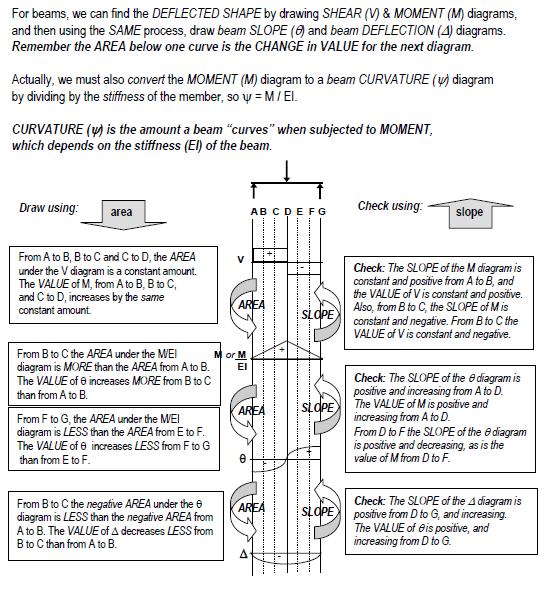
1) Plot the Risa moment diagram into excel, with the x-axis being distance, and the y axis being M/EI and use a best fit line to develop the equation of the line. This should be the angle of rotation if im not mistaken
2) Solve an indefinite integral of the angle of equation formula in terms of x, which will give the equation for deflection.
3) Plot the equation from the indefinite integral of the angle of rotation equation and you will now have the deflection equation.
There is something wrong in this project as I am getting a deflection diagram that doesn't resemble Risa's
Is there an easy way to find a deflection diagram from a moment diagram such as what is given in Risa.
I am attempting now and this is what I have come up with.
1) Plot the Risa moment diagram into excel, with the x-axis being distance, and the y axis being M/EI and use a best fit line to develop the equation of the line. This should be the angle of rotation if im not mistaken
2) Solve an indefinite integral of the angle of equation formula in terms of x, which will give the equation for deflection.
3) Plot the equation from the indefinite integral of the angle of rotation equation and you will now have the deflection equation.
There is something wrong in this project as I am getting a deflection diagram that doesn't resemble Risa's