'''
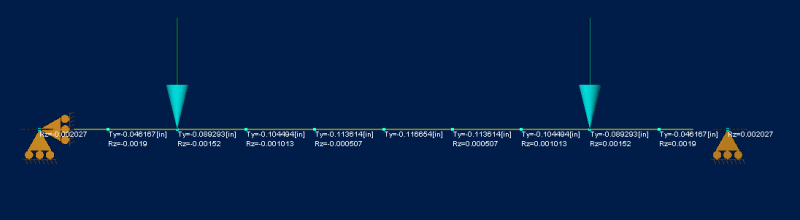
Timoshenko General form equations for a simply
supported beam with an applied Point load anywhere
along the beam span.
Note unlike the Euler-Bernoulli beam formulas
the beam properties are needed as part of the
initial inputs.
** Maintain consistent units among the inputs **
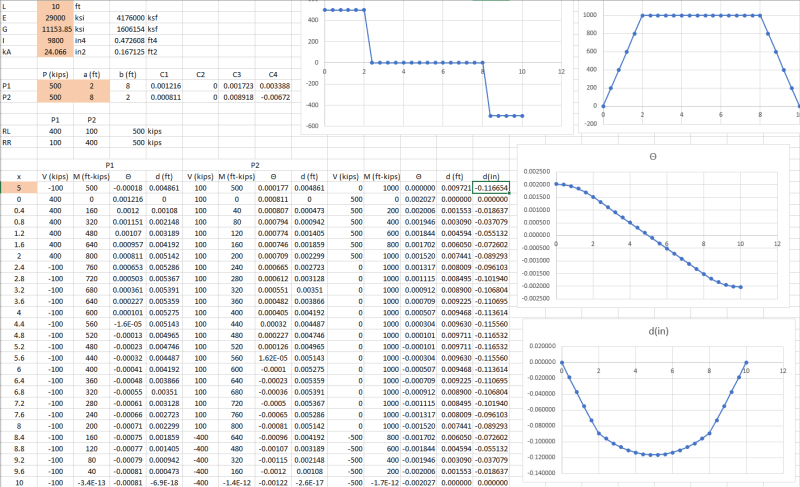
P = load
a = load location from left end of beam
L = beam span
E = beam modulus of elastacity
I = beam second moment of area about the axis of bending
G = beam shear modulus
kA = beam shear area, typically the beam web area for steel W shapes
sign convention:
(+) positive loads are applied in the (-) negative y direction
(+) positive reactions are in the (+) positive y direction
'''
# b = L-a
b = L - a
# Simple End Reactions from statics
# Sum V = 0 and Sum M = 0
rl = (P*b)/L
rr = (P*a)/L
'''
Integration constants
resulting from integration of the two formulas
M = -EI dtheta/dx
V = kAG (-theta + ddelta/dx)
Initial conditions:
delta = 0 at x=0 and x = L
Compatibility conditions:
theta = constant at x = a
delta = constant at x = a
'''
c1 = ((-1*P*math.pow(a,2)) / (2*E*I) +
((P*math.pow(a,3)) / (6*E*I*L)) +
((P*a*L) / (3*E*I)))
c2 = 0
c3 = (((P*math.pow(a,3))/(6*E*I*L)) +
((P*a*L)/(3*E*I)))
c4 = (((P*a)/(kA*G)) -
((P*math.pow(a,3))/(6*E*I)))
if x <= a:
delta = (((rl*x)/(kA*G)) -
((rl*math.pow(x,3))/(6*E*I)) +
(c1*x) + c2)
else:
delta = (((-1.0*rr*x)/(kA*G)) +
((P*a*math.pow(x,3))/(6*E*I*L)) -
((P*a*math.pow(x,2))/(2*E*I)) +
(c3*x) + c4)