Finding the section modulus per Blodgett of a rotate weld shape 1

[cbinder46]

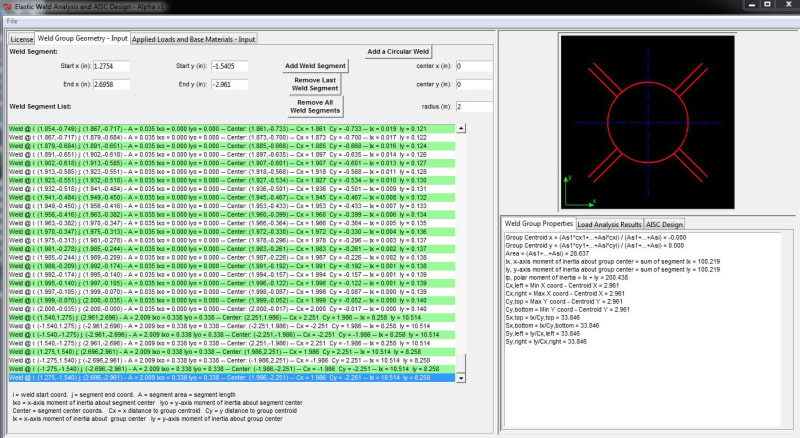
I have been doing weld design per Blodgett's "Design of Welded Structures" and I had a question regarding how to find the Section modulus of the example on page 7.4-14 that involves a pole with a base plate and 4 gusset plates. I looked at my shear and moment acting in the x-axis or y-axis so the section modulus calculated in the example is the same as what I wanted to do. However, when I rotate the loading 45 degrees (now acting between the gussets), I am at a loss for how to find the section modulus. See the photo for what I am talking about.

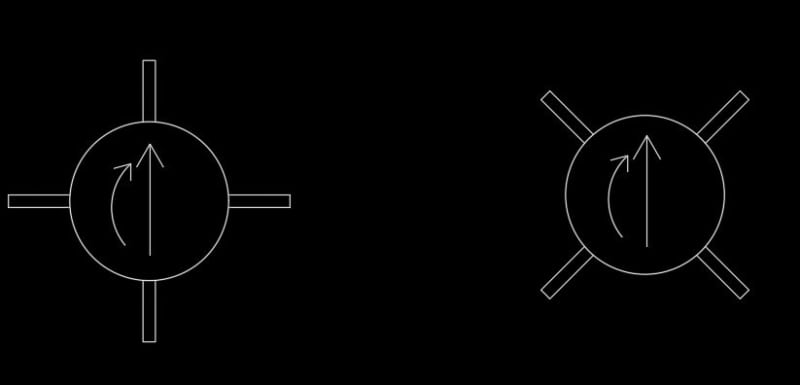
For the case where the loading is acting on the gusset (Left), finding 'I' is broken into two parts. I=(d^3-d1^3)/6 for the gussets, and I=(pi*d1^3)/8 for the pole/base weld line. Sum them up and divide by d/2 to get section modulus (S). 'd' is out diameter and 'd1' is inner diameter.

I do not understand how to find the I's for a rotated case.

 

[Ron]

Ignore the gussets for adding bending strength to your round section....it is doubtful your bending moment is significantly different at the bottom of the round section as compared to just above the top of the gusset where the gusset would have no bending influence anyway. Resolve the forces in the welds as only shear and tension.

 

[robyengIT]

please check here for "Welding formulas and tables - Hobert" (page 1 and 2). You can download it with the link of the last post (Slideruleera)

 

[TimSchrader2]

HELLO Most CAD programs like ACAD mechanical have the calculate inertia feature pull downs.

Or to calc by hand by the parts, you can use (I about centroid) + (A x Yc squared) for each part. Yc being dist form centroid of group of parts. As you may have done for first case. The Ic of gusset at 45deg should be close to (Thickenss x h cubed)/12) x sin 45. this may not be a conservative simplying assumption.

OPT 1 or look up it the above references and then use that in your calcs of inertia parts if you need a exact non conservative answer. Conservative Calcs will usually be much quicker as long as they do not get you into a "over kill" design. If gussets are short this is all academic as noted by above. By Ron

 

[cbinder46]

I think I may have not been clear. I am looking to find the Ic of the weld lines for the structure of this shape. So Ic will be in units of length^3 not length^4. RobyengIT had a good resource, I was looking at case 23 (see photo below) and I had a question. Would the Ic be greater in the left (from the original picture above) case or the right case? I was leaning toward the left yesterday, but today I am leaning to the right now.

 

[robyengIT]

case 22 : Ix = Iy'

 

[BMart006]

Your post is a little confusing as to whether you are looking for the polar moment of inertia or section modulus of the weld (treated as a line). In either case, you first need to calculate the moment of inertia of the weld shape about two mutually perpendicular axes, x and y. For example, two parallel welds of width "b", "d" distance apart of weld size "a" will have Ix = 2*(1/12*b*a^3) + 2*(b*a*(d/2)^2) and Iy = 2*(1/12*a*d^3). Because a is small compared to b and d, a^3 is considered negligible; Ix = 2*(b*a*(d/2)^2). The section modulus will be the moment of inertia of whichever axis divided by the distance from the neutral axis (weld CG if bearing is neglected) to the extreme fiber. Therefore, Sx = Ix/(d/2) and Sy = Iy/(b/2). The polar moment of inertia (Ic or Jw) = Ix + Iy. Do this exercise for a few weldments and you'll find they match Blodgett's book.

 

[Celt83]

think of the welds as rectangles with a unit width and depth d. If you have a the 13th edition of the steel manual handy the formulas for a weld line at an angle are noted in the top right of figure 8-6 on pg 8-13. Combining everything is just a matter of utilizing the parallel axis theorem

Here are the properties I come up with for a 4" diameter circle and 2" long x 3/8" thick gussets at 45 degree increments:
(the last 8 rows in the table are the gusset weld properties the others are for segments of the circle)

Open Source Structural Applications:

https://github.com/buddyd16/Structural-Engineering

 

[spats]

I found this in the handout material I received when I took Blodgett's course many years ago.