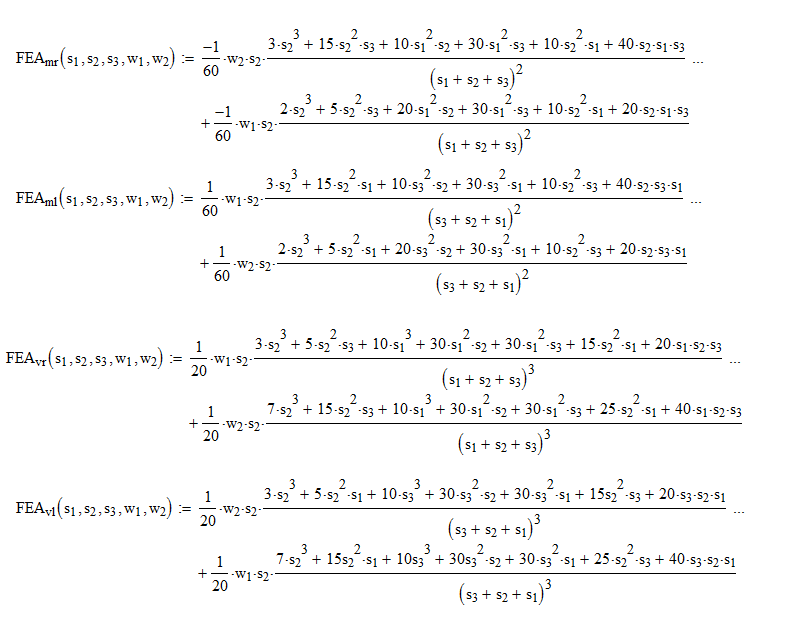TarikHKJ
Structural
- May 8, 2016
- 79
Hi,
Trying to solve an indeterminate beam using moment distribution displacement method, I used the general fixed-end moment equations, but one span has a trapezoidal load on part of the span which does not have a fixed-end moment equation,
here is the problem:
How to calculate the fixed-end moments for that span?
Many Thanks!
Trying to solve an indeterminate beam using moment distribution displacement method, I used the general fixed-end moment equations, but one span has a trapezoidal load on part of the span which does not have a fixed-end moment equation,
here is the problem:
How to calculate the fixed-end moments for that span?
Many Thanks!