Chrissy123
Mechanical
According to ASME there is a calculation for flat head thickness (t) with the equation shown below. Is this applicable regardless of the ratio of head thickness to cylinder thickness ? I have a pressure vessel where the shell thickness of the cylinder is 100mm and the head thickness is 10mm, length of cylinder is 508mm, inner radius 254mm, The calculated allowed pressure value seems very low - in the region of 0.24 MPa (using C=0.33, yield strength 207 MPa) - does that seem a reasonable allowable pressure for such a design ?
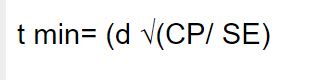
thanks,
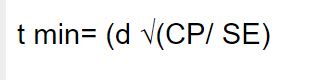
thanks,
