MatthewMansfield
Civil/Environmental
- Aug 11, 2012
- 47
Hello all
I was hoping someone could clarify the difference between the equations both of which tells me the force due to water
The first equation, I think was to calculate the total force acting on a wall caused by a fluid in this case water:-
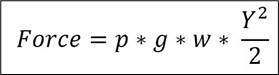
Where:-
p = density
g = gravity
w = width of wall
Y = height of the water on the wall
The second equation I have been told tells me the force acting on a submerged object:-
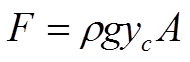
Where
F = Force
p = density
g = gravity
yc = Distance from water surface to the centroid of the submerged object
I am really struggling to understand the difference between the two equations and I was hoping you could or anyone else could shed some light - to me they should be the same.
Thanks
I was hoping someone could clarify the difference between the equations both of which tells me the force due to water
The first equation, I think was to calculate the total force acting on a wall caused by a fluid in this case water:-
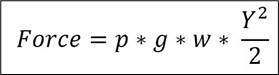
Where:-
p = density
g = gravity
w = width of wall
Y = height of the water on the wall
The second equation I have been told tells me the force acting on a submerged object:-
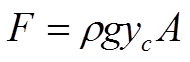
Where
F = Force
p = density
g = gravity
yc = Distance from water surface to the centroid of the submerged object
I am really struggling to understand the difference between the two equations and I was hoping you could or anyone else could shed some light - to me they should be the same.
Thanks
