Agunia
Student
- Dec 29, 2020
- 4
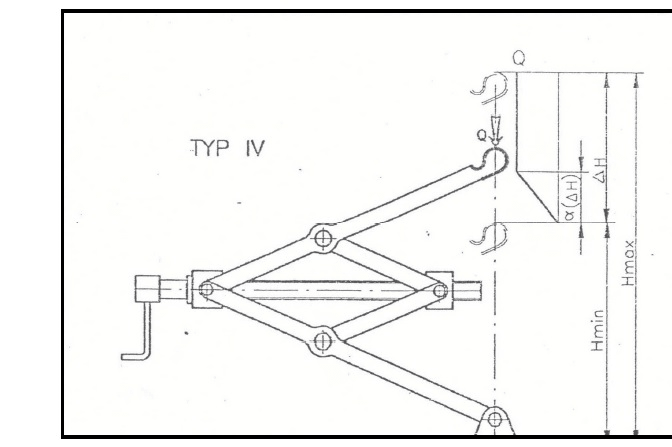
Hi
I need help, how can i calculate force in screw and in rods ?
Follow along with the video below to see how to install our site as a web app on your home screen.
Note: This feature may not be available in some browsers.
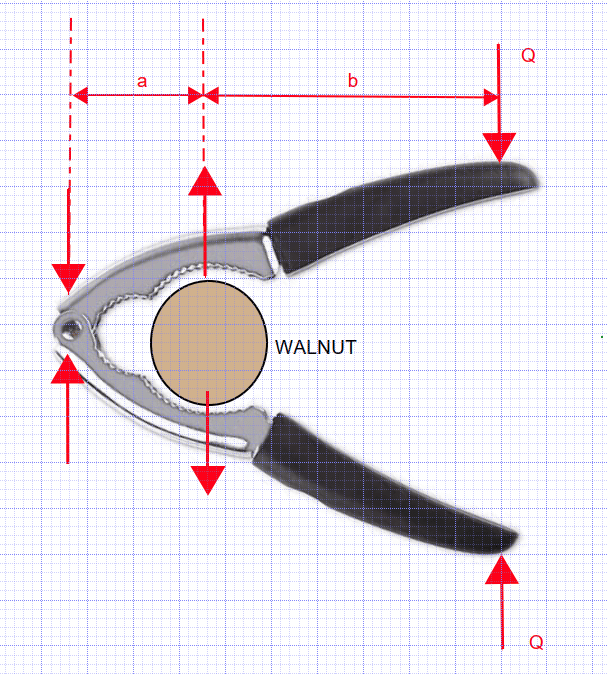
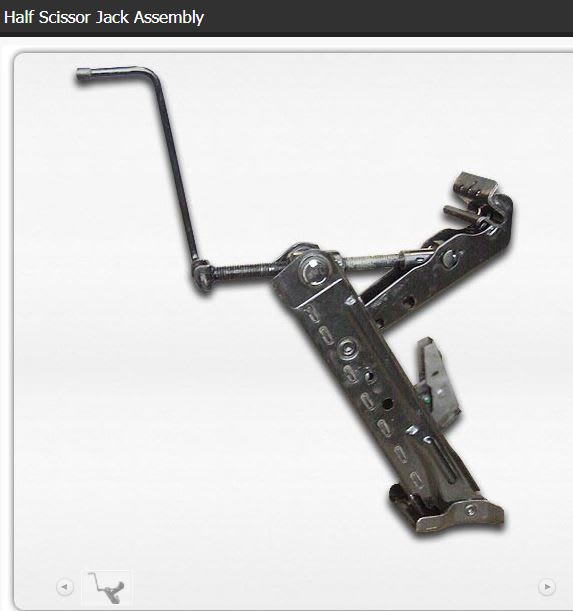
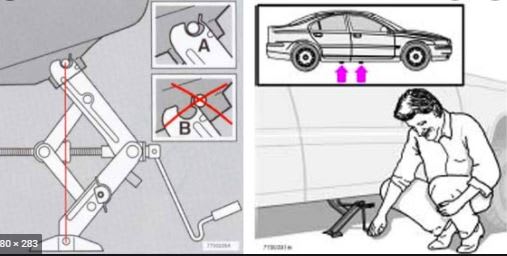


GregLocock said:It is stabilised by the wheels on the other side of the car, although I agree it isn't ideal.
