Forces on a slope 1

[jadams62]

This is going to sound like a home work problem but I promise it isn’t!

My boss has given me a task (anyone that reads the automation posts will be aware of this) and there is one final part of it I need to show and that is the forces acting on a door I have to design, I know this is simple but it’s not my area so I don’t really have any idea, anyway:

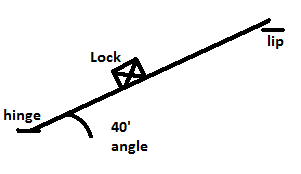
If I have a mass on a slope at a 40' angle, what forces are acting on the slope (not the mass)

Basically the door hinges (horizontal hinge) and it has a hefty electromagnet lock on it (about 2 kg), in the centre, and so when the door is open at 40'degrees what forces are the lock exerting on the door

It looks like this: (dotted lines are the dor 'o' the hinge and M is the lock.
.
M .
.
.
O
Is it just a vertical force?

Cheers

 

[cloa]

So the hinge locks at 40 degrees or the electromagnet is keeping the door from opening more? This door opens downwards?

 

[jadams62]

hmm, my little drawing didnt look anything like that when i typed it...

Ill try explane it better, the door is horizontal when closed (and locked with the mag) and swings back on its self (upwards) and round so it is 40 degrees to the horizontal, there is a lip that supports it in that position.

Thanks

 

[desertfox]

Hi

Assume you have a mass on a 40 degree slope, you have the vertical mass which multiplied by 9.81 gives the vertical force. Now you can resolve that force into two forces- one acting perpendicular to the slope and the other parallel to the slope.

parallel = mass * 9.81 * sin 40

perpendicular mass * 9.81 * cos 40

 

[jadams62]

Thanks, here is a picture to elimiate any confusion

 

[zekeman]

Well, in the absence of friction, you use the 3 force-moment equilibrium equations ; but with 4 unknowns, namely the horizontal and vertical forces at the hinge and the lip, you need one additional equation for a solution.
Hint:
From the geometry of contact at the lip, you should be able to write the 4th equation relating the 2 forces at the lip.
If you are an engineer, a solution should be straightforward.
With friction, it gets more complicated, but I don't think your boss needs that answer.

 

[jadams62]

Thank you.

Can you explain what the '3 force-moment equilibrium equations' or perhaps a link explaining it?

 

[zekeman]

2 forces Fi and Fj, the orthogonal components of the hinge force
Fi along the door
Fj perpendicular to the door
Fl lip force assumed perpendicular to the door

lock mass force components
along door Mg*sin(40)
perpendicular to door Mg*cos(40)
M mass of door in kg
g gravitational constant 9.8 meters/sec/sec
Mg gravitational force in Newtons
sum forces along door= 0
(1) Fi-Mg*sin(40)=0
Sum forces perpendicular to door
(2) Fj-Mg*cos(40)+Fl=0
clockwise Moment equation
around hinge
(3) Mg*cos(40)*L-Fl*K=0
L= distance along door from hinge to lock
K = distance along door to lip contact point
3 equations and 3 unknowns, Fi,Fj,Fl
I think (hope) you can solve it for F1 and Fj, the hinge force components
The total hinge force would then be
the square root of the sum of the squares of Fi and Fj.

 

[rb1957]

research "free body diagram" and "equations of equilibrium"

in you case i think you only have to worry in-plane forces ... so (as zeke says) you have two sets for forces to balance (Fx and Fy) and one set of moments (Mz).

i think the weight force will act down whihc would give two vertical reactions (one at the hinge, one at the lip).
you can equate these vertical forces to components in the direction of the door (cos40, sin40)