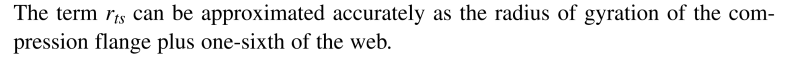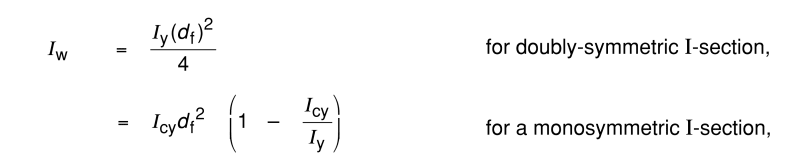Formulae for rts and J for modified wide flange

[Iasonasx]

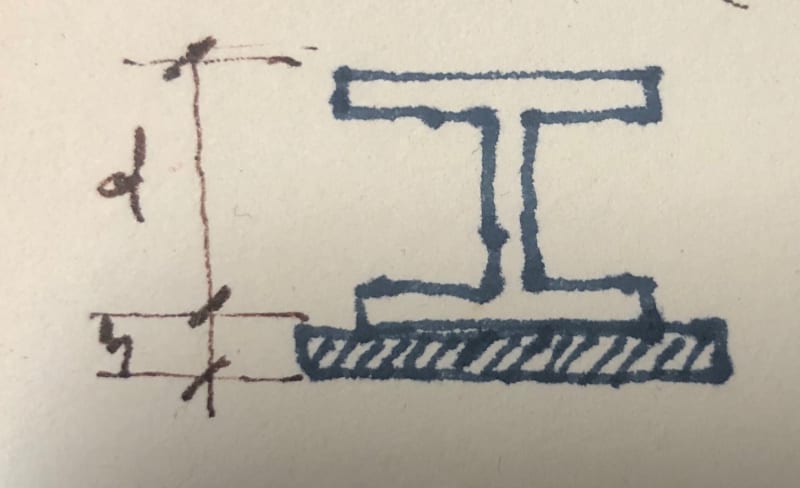
We have old steel elements that need to be enhanced with a steel plate on the bottom to support new equipment in an old building. We consider welding a plate on the bottom. When it comes to NA, new Ix, Iy, rx, ry etc, that's easy pasy. I am stuck with which formulae would be applicable for the J (torsional constant) and the rts. The AISC 15th edition manual is giving us something on pg. 161-49 but I am reluctant to use that as we don't actually have a symmetrical element since the bottom flange is going to be way thicker now. For J, again, the top and bottom flanges are not identical, so is there a formula that would be applicable?.

 

[Agent666]

To get an accurate answer you really have to resort to FEA to work out torsion and warping constants. I recommend this python package if you're after a free open source means of doing this, if you're familiar with python of course (but if you check the read the docs page there are plenty of examples to get you started). If you provide the dimensions I'm even happy to provide a script to get you started.

I have seen a simple formulation somewhere but can't recall where (in relation to adding channels to top of I-sections for crane runway beams and estimating the resultant J), whereby you simply equate the flange and strengthening element to an equivalent thickness single plate and do the old J = sum(bt^3)/3 for an open section for all the plates making up the I section including the strengthening plate. Obviously, this type of simple formulation negates the benefit of the root radii which can actually add a lot to the torsion constant in I-sections.

Not sure what you mean by 'rts'? Can you elaborate?

https://engineervsheep.com

 

[WARose]

For multiple pieces in a cross section: J= ∑(bt[sup]3[/sup]/3)

where:

b=length of each cross-sectional element
t=thickness of each cross-sectional element

This formula is (of course) a approximation....but I have found it to be sufficient in most cases.

I'm not sure what "rts" is either.

 

[Iasonasx]

rts is a gyration radius that we can see in the shapes section of the AISC. It is the fourth last column for every W section.

 

[Agent666]

Ok got it now (AISC not my local code), there is a formula in the AISC code for this isn't there? For example, check section F2?

You will of course need Cw the warping coefficient for this, and then you're essentially back at needing an FEA solution for an accurate answer. Unsure if the formula given extends to the case of the plate on the bottom with an equivalent larger flange as a monosymmetric beam.

There is this approximation noted in the code, but I assume it only applies to doubly symmetric I-sections:-

https://engineervsheep.com

 

[Iasonasx]

Exactly, the absence of symmetry along the XX axis through the introduction of the welded plate should alternate the above which is based upon the assumption of that symmetry. I am not sure what portion would qualify but I think that the rts is more of an empirically established value.

 

[Agent666]

You don't really need r_ts per say (it's just an intermediate calculation to simplify the LTB equation), you really need C_w. For that you'll need to resort to an FEA approach, or you could try your luck at using the following. This is from my own local code for a monosymmetric I section: -

Never really tested the formula as I almost always determine the properties using an FEA approach.

But if you provide your section and plate I can run it in the previously mentioned sectionproperties package and compare to your hand check?

https://engineervsheep.com

 

[Iasonasx]

That would be very kind but there is a series of sections that will be treated like that so I cannot have you do my work in the end. Thank you again!