Davy Pee
Mechanical
- Dec 6, 2023
- 3
Hey Eng-Tips,
I have a device mounted on a wall, which I'm trying to see if it can support. I have applied load P1 at the end, and component weight applied in the center, P2, at L1 and L2, respectively. The device has two supports, A and B, which I'm trying to find the horizontal reactions for, if any.
Thanks
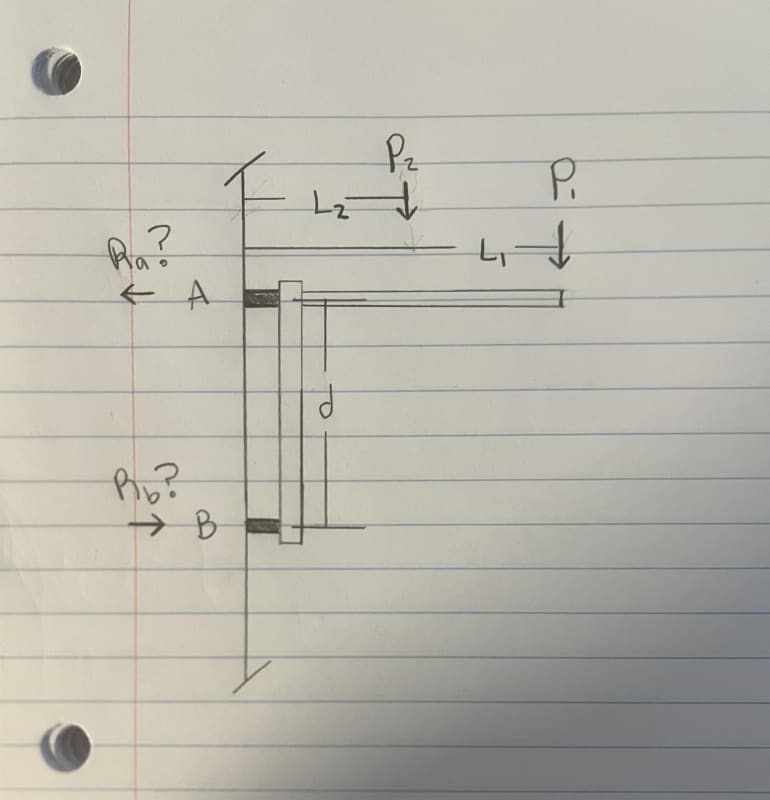
I have a device mounted on a wall, which I'm trying to see if it can support. I have applied load P1 at the end, and component weight applied in the center, P2, at L1 and L2, respectively. The device has two supports, A and B, which I'm trying to find the horizontal reactions for, if any.
Thanks

