Full tank being emptied - Bernoulli 1

[Peter C]

Hello,

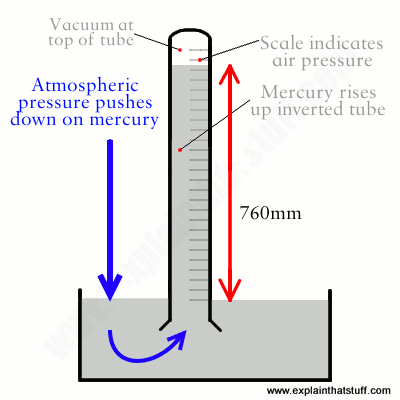
Very commonly people we hear that a tank where column pressure is not big enough to overcome Patm will not empty by itself. In my opinion, most of those who say that forget that once the tank was open to be fulled and, therefore, we must add 1atm pressure to the fluid at any point.

So lets consider the following case: 1) a tank of height H is completly empty, 2) fluid (water in this case) is being pumped in through a valve in the bottom side while air is comming out at the top side, 3) once the tank is completly full, both valves are closed and 4) the valve at the bottom is opened.

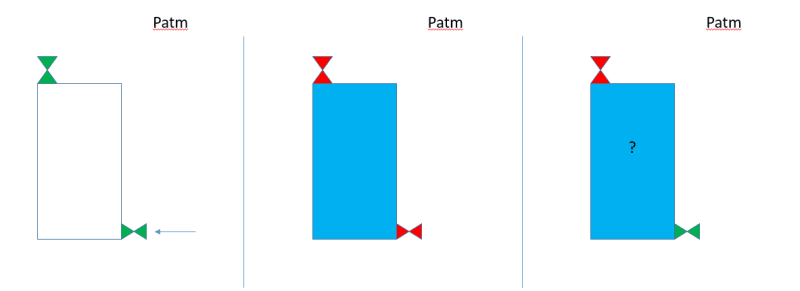
When the valve at the bottom is opened, what happens with the fluid inside? Will some of it come out, creating a "void' in the top of the tank (p = pvapor of the fluid)? NOTHING will come out? It will completly empty?
For now, lets ignore that air bubbles may come in from the bottom.

Can you answer using Bernoulli?

Regards

 

[1503-44]

I would ignore the transient dynamics and treat this as a fluid statics problem. Bernoulli not really required. When inside pressure at the outlet equals atmospheric pressure, flow stops.

If the water level inside the tank is less than 32.5 ft, basically nothing, or very little water comes out, as atmospheric pressure is slightly higher than pressure at the interior of the outlet valve. If the water level is greater than 33ft, the tank will drain creating a vapor space above the liquid. Interior pressure above the water surface will equal the vapor pressure of the water. Around 0.5 psia or so at normal ambient temperatures. The tank will drain to approximately a 32.5 ft height above the outlet nozzle. At that level interior pressure at the outlet nozzle equals
0.5 psi vapor pressure + 32.5ft x 62.4/144 = 14.58 psia, roughly the same as standard atmospheric pressure. Pressure at the nozzle equalises and drainage stops. No more water will exit the tank, unless the tank buckles at the roof and wall seam from the vacuum created inside and the tank collapses, or without pumping air into the outlet at the bottom, or letting air in through the top valve.



--Einstein gave the same test to students every year. When asked why he would do something like that, "Because the answers had changed."

 

[LittleInch]

Totally agree with Mr44.

Only thing to add is the height is dependant on the water temperature and hence vapour pressure.

There will be a few drops due to Bulk modulus of the water, I.e. water is almost but not quite incompressible. So maybe about 0.001% of the volume or something like that.

Remember - More details = better answers
Also: If you get a response it's polite to respond to it.

 

[Peter C]

I agree that no water would come out if level is under 32ft, yet I can't explain using just static equations.

For me, pressure at the bottom of the tank will not be lower than the ATM pressure. In fact, pressure at the bottom will be 1atm + column height. As a reminder, tank was filled with a venting on the top, so at any point the liquid total pressure would be
patm + rho*g*h. Therefore, that's always greater than patm...

For me, what stops fluid from coming out is the vacuum that is created at the top when fluid tries to flow out, but i can't put that into equation.

What do you think?

 

[1503-44]

Basically your tank acts like a barometer.

Since you have water in the tank, it needs the 33ft level.
If you have Mercury, it's only 29.92 inches tall.

--Einstein gave the same test to students every year. When asked why he would do something like that, "Because the answers had changed."

 

[1503-44]

OK, right. Let's say, when you start to open the valve, the pressures are exactly equal at the outlet valve.

Because you filled the tank from the bottom and maybe not vented out the total amount of air trapped at the top, that is exactly what will allow some water to drain out. When you open the bottom valve, that air will expand at the top of the tank until it equals the water's vapor pressure. That expansion of the air allows water to flow out. That outflow will continue until pressures are balanced at the bottom valve.

If say there was 1 cubic foot of air at the top of the 33ft high tank. Reducing the pressure to 0.5 psia causes that volume of air to increase ...

1 ft3 x 14.67 psia (atm pressure) /0.5 psia (water vapor pressure) = 29.3 ft3
So that amount 29.3 ft3 of water exits the tank.

Now you have to see how the exit of 29.3 ft3 of water affected the water level in the tank.
It probably reduced the level (don't know the tank's area, so not sure how much.)

Let's say the tank area is 10ft2, making the loss of level = 29.3/10 = 2.93 ft
Water height is 26.37 ft
Now inside the outlet valve the pressure is 0.5 psia + 26.37 ft x 62.4/144 = 11.9 psia
It is now much lower than 14.67 atm pressure outside. (I had that moment in mind when I said less than atm pressure.)

OK, so what happens now?
Pressure inside is less than outside. Air goes in? No, it cannot, water is coming out.
When the water stops coming out, if air can get in, maybe some more water comes out. If air can't get in, flow remains stopped.

So, it is very important to fill the tank completely with water, displacing all the air, before starting this experiment.

Continuing with this simulation of the practicalities of tank draining in real life, now can get somewhat complicated.

Note that there is a small pressure loss at the outlet valve, due to valve friction and outlet pipe geometry, but it occurs only when water is flowing (out), or air is flowing (in), and we have ignored that That pressure loss is 0 before flow starts and could be significant at maximum flow, maybe up to H/2 thereby reducing the outlet pressure of the valve well below atm pressure. Of course then atm pressure will tend to stop that outflow even more as outflow increases. This is where you might want to consider Bernoulli effects. There is potential for a lot of gurgling and spurting to go on as atm pressure tries to balance tank pressure and resulting outflow. Where does it stop? If any air gets in, it won't. That is difficult, so it usually stops, but nothing is totally sure at that point.

--Einstein gave the same test to students every year. When asked why he would do something like that, "Because the answers had changed."

 

[Compositepro]

That's a lot of thinking out loud there about irrelevent factors like bulk modulus and air. There is no air in the tank. Water can be considered non- compressible for this discussion. When you open the valve in the bottom the pressure at the top of the tank drops from one atm by the amount of (rho)(g)(h). If this pressure is less than the vapor pressure of water, then a void will form at the top of the tank, and water will flow out until the bottom pressure is one atm. For this discussion vapor pressure and dissolved air can also really be neglected. Just say that the pressure is essentially zero absolute pressure after the bottom valve is opened.
Bernoulli is an energy balance equation involving potential energy of pressure and height, and kinetic energy. With no kinetic energy involved here, it simplifies to a force balance equation involving height and pressure.

 

[LittleInch]

"so at any point the liquid total pressure would be patm + rho*g*h.

I think this is incorrect.

It is patm - rho*g*h, with h measured from the bottom.

Therefore at the bottom the pressure is atmospheric, but at the top it is lower. You cant get lower than zero

Remember - More details = better answers
Also: If you get a response it's polite to respond to it.

 

[1503-44]

" so at any point the liquid total pressure would be patm + rho*g*h."

I think that is true. If you filled the tank without purging all the air and then closed all valves, the tank is a pressurised tank (in terms of absolute pressure), air pressure = 1 atm. At lower points its + rho g h.

That is why water exits the tank, if all air is not purged out. The same way the barometer works. You must allow for the surface level in the cup to vary as the atmospheric pressure changes and affects the volume in the tube. Mercury enters and leaves the tube and its height changes corresponding to the momentary atm pressures. A barometer with air trapped at the top is not very accurate at all. I had to turn the tube upside down and fill it with Mercury, put my thumb on it and invert the tube, placing it (and my thumb) into the cup of Mercury. Then it would read correctly.

If there is no air inside, then no (little) water exits, as the pressure almost immediately becomes vapor pressure when the outlet is opened. It is not exactly immediately, as there are vaporisation rates that should be considered, if you want to look at the milisecond scale. Stoner Pipeline Simulator Operating Manual explains all of that in conjunction with predicting vapor formation and collapse rate when fluid in a pipeline oscillates around vapor pressure. Availability of Heat of vaporisation and condensation must be incorporated (with a fudge factor) to get the simulation tuned to match observed fluid column collapse pressure waves. The simulator isn't very accurate without that tuning, but does tend to give higher pressures and faster times without the tuning.

--Einstein gave the same test to students every year. When asked why he would do something like that, "Because the answers had changed."

 

[1503-44]

" so at any point the liquid total pressure would be patm + rho*g*h."

I think that is true. If you filled the tank without purging all the air and then closed all valves, the tank is a pressurised tank (in terms of absolute pressure), air pressure = 1 atm. At lower points its + rho g h.

That is why water exits the tank, if all air is not purged out. The same way the barometer works. You must allow for the surface level in the cup to vary as the atmospheric pressure changes and affects the volume in the tube. Mercury enters and leaves the tube and its height changes corresponding to the momentary atm pressures. A barometer with air trapped at the top is not very accurate at all. I had to turn the tube upside down and fill it with Mercury, put my thumb on it and invert the tube, placing it (and my thumb) into the cup of Mercury. Then it would read correctly.

If there is no air inside, then no (little) water exits, as the pressure almost immediately becomes vapor pressure when the outlet is opened. It is not exactly immediately, as there are vaporisation rates that should be considered, if you want to look at the milisecond scale. Stoner Pipeline Simulator Operating Manual explains all of that in conjunction with predicting vapor formation and collapse rate when fluid in a pipeline oscillates around vapor pressure. Availability of Heat of vaporisation and condensation must be incorporated (with a fudge factor) to get the simulation tuned to match observed fluid column collapse pressure waves. The simulator isn't very accurate without that tuning, but does tend to give higher pressures and faster times without the tuning.

--Einstein gave the same test to students every year. When asked why he would do something like that, "Because the answers had changed."

--Einstein gave the same test to students every year. When asked why he would do something like that, "Because the answers had changed."

 

[Peter C]

So indeed there are two different force balances: 1/ when the valve is closed: at that point the pressure at any given point is 1atm + p*g*h from h mesured from the top to the bottom ; 2/ once the valve is opened, there is an equalization at the bottom pressure and the external pressure (because they are at the same "level" and therefore the pressure at any given point is now 1atm - p*g*h from h being mesured from the bottom to the top.

A second question arises: we see that clearly the "total pressure" in the tank has decreased, so there must have some work done for the energy conservation sake. What work has been done if water doesn't flow out? Is it its decompression and therefore a minimal dilatation?

 

[1503-44]

When the valve is closed there are two separate pressures, that inside the tank and that outside.

When the valve opens,
If there is some air inside the tank, internal pressure is atm + rho g h
External pressure is only atm.
Inside pressure is greater, so water exits, air expands and water level drops to where internal and external pressure balance is achieved.

BUT

IF there is no air inside the tank, internal pressure is vapor + rho gh.
That means that
If H is 32.5ft or greater, internal pressure is greater than external and some water exits. Water level will drop to about 32.5 ft.
However, IF H is initially <= 32.5 ft, internal pressure is <= atm and no water exits.

--Einstein gave the same test to students every year. When asked why he would do something like that, "Because the answers had changed."

 

[1503-44]

The tank contains potential energy of rho g H
If the level of the water drops by h
Work is volume of water leaving the tank x Density x h, the drop in level.

--Einstein gave the same test to students every year. When asked why he would do something like that, "Because the answers had changed."

 

[pierreick]

Wow!
If you are a student, you should post in the relevant forum.
If you want a simple experimentation, take a plastic bottle, fill it with water, seal it, make a pin hole at the bottom and observe,
No driving force, no flow
unscrew the cap, observe, driving force is Ro*g*H, seal the bottle again and observe.
my 2 cents
Pierre

 

[1503-44]

https://www.britannica.com/science/scientific-method[/URL]]In a typical application of the scientific method, a researcher develops a hypothesis, tests it through various means, and then modifies the hypothesis on the basis of the outcome of the tests and experiments.

He is at phase 1.
Standby for phase 2


--Einstein gave the same test to students every year. When asked why he would do something like that, "Because the answers had changed."

 

[Snickster]

So indeed there are two different force balances: 1/ when the valve is closed: at that point the pressure at any given point is 1atm + p*g*h from h mesured from the top to the bottom ; 2/ once the valve is opened, there is an equalization at the bottom pressure and the external pressure (because they are at the same "level" and therefore the pressure at any given point is now 1atm - p*g*h from h being mesured from the bottom to the top.

Look at it this way. If you have a system of solids or liquids with forces acting on it, or anything composed of matter, and it is not moving, then the sum of the forces acting on it is in balance. Sum F = M*A = 0 per Newtons laws.

For the case with the tank filled with water at atmospheric pressure then closing the valve, the sum of forces of the residual atmospheric pressure plus the liquid height is the pressure at the bottom of the tank. So P = atm + rho*g*h. Since the fluid is not moving with the valve closed then the opposing balancing force is being applied by the valve. So the force of the fluid on the valve is equal to the force of the valve on the fluid and F = M*A = 0.

At the instant the valve is opened the force of the fluid at the valve = atm + rho*g*h times outlet pipe crossectional area is now opposed only by the force of the atmospheric pressure acting on the fluid times the crossectional area of the outlet pipe. So (atm + rho*g*h*)*(Area Outlet) is greater than atm*(Area Outlet). Since sum of force is not equal to zero then acceleration and movement of the fluid will occur and fluid will flow out of the tank by conversion of potential energy of the differential in pressure force into kinetic energy.

The flow will continue until the forces again are balanced. As the fluid flows out of the tank there is a vacuum created at the top of the tank that is filled by the vaporization of the liquid which is at the vapor pressure of the liquid for the given temperature. At about 80 F this is about 0.5 psia for water vapor pressure as stated. So forces will be balanced again when (0.5 + rho*g*h(new))*(Area Outlet) = atm*(Area Outlet) all stated in terms of psia.

A second question arises: we see that clearly the "total pressure" in the tank has decreased, so there must have some work done for the energy conservation sake. What work has been done if water doesn't flow out? Is it its decompression and therefore a minimal dilatation?

The difference in pressure when valve was opened cause the fluid to accelerate by Newtons Law, Sum F = M*A and thereby converting potential energy to kinetic enegy as it flowed out of the tank.

 

[Peter C]

@all thank you for your valuable comments. I'm indeed aware of the bottle experiment. Bit I'm trying to model the problem first. Besides, a pin hole won't let any flow indeed once the bottle is closed, but a big hole will...

@Snickster, thank you for that detailed answer. Indeed that was what I thought at first when I wrote the thread. But for any tank height under 10m, one would never reach the equilibrium of Pvapor + p*g*h = patm. If Pvapor = 0,5 psi and Patm = 14,7, therefore p*g*h = 14,2 psi. If my liquid is water and I have a height of about 5m for exemple this equality will never be true... Do you agree?

 

[1503-44]

In that case you can't just say you have 5m, unless that is the height of the tank. Atm pressure will fill the tank to 10m level, so any tank <10m tall should be full, If its not full, then you probably have air trapped inside.

If the tank is 11m High...
Assume the pressure inside and outside the valve are equal, there is no visible flow of air in or water out, then solve for h. Look at the barometer problem where the "hole diameter is infinite". Solving for h, you will see the water should be at 10m. If you do see only a 5m height, something is wrong; the valve is closed, or maybe it is because there is air trapped inside. Now calculate the amount of trapped air inside the tank, assuming a tank area of 10m2

Pressure inside the tank at the water surface is
1 Bara, atm pressure outside the tank
-5m water inside the tank = 0.5 Bara
= 0.5 Bara at the water surface

Empty space inside the tank
(11m-5m) x 10m2 = 60m3
Pressure = 0.5 Bara

PV = n RT
T = 20°C ?
P = 0.5 Bara
V =60m3
R= 0.08314 kg⋅m3 /°K /mol
T = 293 °K

n = PV/R/T

https://www.gigacalculator.com/calculators/ideal-gas-law-calculator.php

1231 mol of air

Actually it's a bit less air, due to the amount of water vapor making up the total volume which I ignored.


--Einstein gave the same test to students every year. When asked why he would do something like that, "Because the answers had changed."

 

[Peter C]

But what if the tank is 5m high?

 

[1503-44]

See line 2 above
"so any tank <10m tall should be full, If its not full, then you probably have air trapped inside."

Trapped air under pressure, or the tank roof, is what is preventing any water from entering and reaching a level of up to 10m.

In which case you can calculate the amount of air inside using the same formula.

If the tank is 5m tall and you have a 4m water level, then volume of space is (5-4) x 10m2 = 10m3
Pressure in the space is 1 Bara atm - 4m x 1 Bar/10m = 0.6 Bara

If there is no air, then you simply have a water level = height of tank.
The water has a pressure of 0.5 Bara at the tank roof and 1 Bara at the outlet valve.

--Einstein gave the same test to students every year. When asked why he would do something like that, "Because the answers had changed."