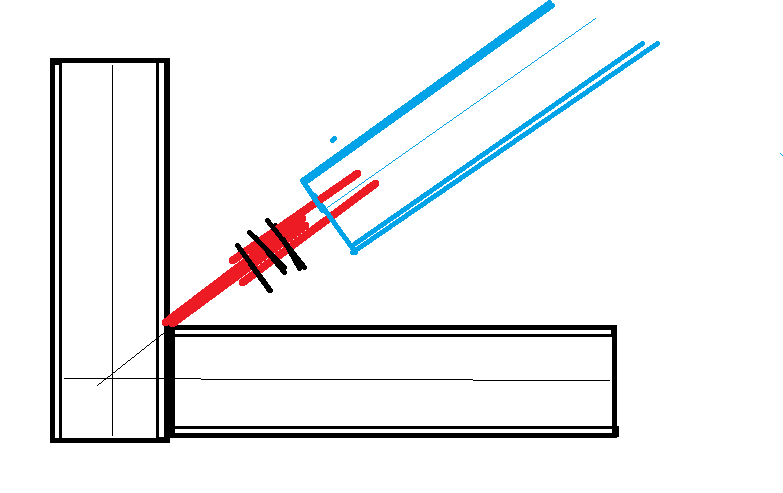
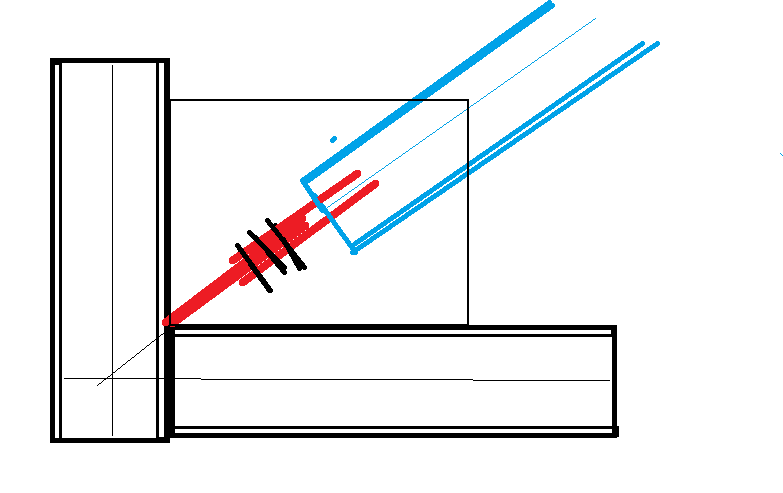
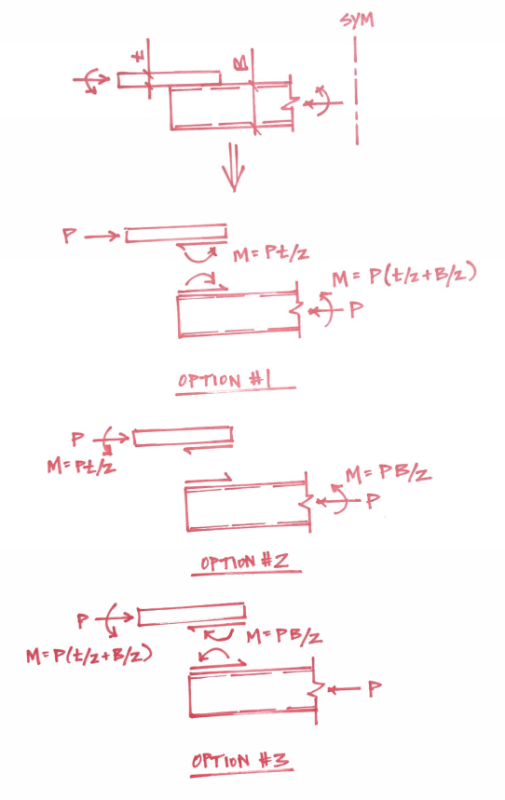
I have a new project to design bracing for an existing building. The force in the bracing is Cf = Tf = 103K... big forces!
The problem is that the gusset will be secured at the centroid of the resisting beams and columns because there is an existing masonry wall located to the centerline of the connection. The EOR want me to design the connection for an HSS 10x4x0.5 (located at the face of the wall), welding the HSS to the face of the gusset, creating an eccentricity of 2" (from the HSS) + half the thickness of the gusset.
I've designed it using elastic combined stresses, based on a Whitmore width for compression. If it weren't for the compressive load, I'd have used the plastic section. I'm looking for some comments how others would design this for the eccentricity. I've suggested going to plate that is roughly 1"x12", in lieu of the HSS, to minimise eccentricity or possibly using the existing masonry wall for lateral forces.
Rather than think climate change and the corona virus as science, think of it as the wrath of God. Do you feel any better?
-Dik
The problem is that the gusset will be secured at the centroid of the resisting beams and columns because there is an existing masonry wall located to the centerline of the connection. The EOR want me to design the connection for an HSS 10x4x0.5 (located at the face of the wall), welding the HSS to the face of the gusset, creating an eccentricity of 2" (from the HSS) + half the thickness of the gusset.
I've designed it using elastic combined stresses, based on a Whitmore width for compression. If it weren't for the compressive load, I'd have used the plastic section. I'm looking for some comments how others would design this for the eccentricity. I've suggested going to plate that is roughly 1"x12", in lieu of the HSS, to minimise eccentricity or possibly using the existing masonry wall for lateral forces.
Rather than think climate change and the corona virus as science, think of it as the wrath of God. Do you feel any better?
-Dik

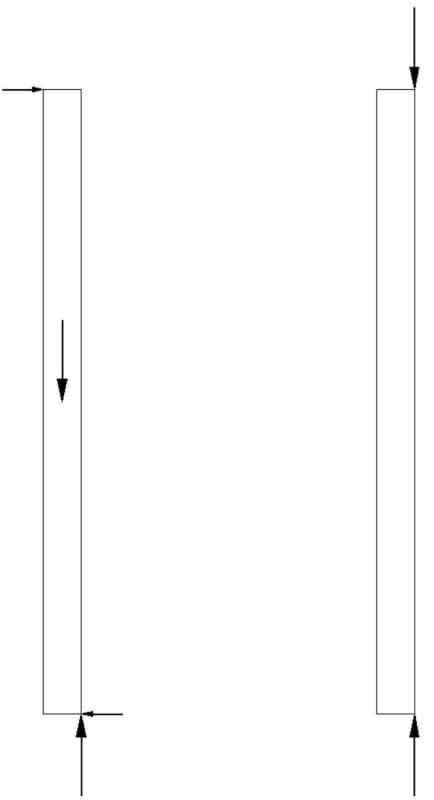
![[smarty] [smarty] [smarty]](/data/assets/smilies/smarty.gif)
![[ponder] [ponder] [ponder]](/data/assets/smilies/ponder.gif)