Dear all,
I just found that I made a horrible mistake in my calcualion for a phase chaning heat exchanger desing. For the design i wanted to include the change in physical properties, for which I decided to create the heat exchanger in a discretized manner. I did this and calculated the heat transfer coefficient on each side, which was no problem. but depending on the step size I chose, the entire length of the heat exchanger varies, since the formula for the overall heat transfer coefficient apparently can only be used on the total length of the exchanger, which is of course not possible since it is unknown.
The formula I used for the overal heat transfer coefficient is the following:
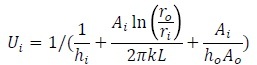
The areas Ai and Ao I calculated are of course in the discrete way of my design a function of the stepsize dx. With this the overall heat transfer coefficient changes strongly with stepsize, leading to a different length of the overall exchanger (I fixed a required output temperature, based on the saturation temperature of one of the fluids).
Now I dont know how I can calculate the change in heat of the fluids. Before I was using the following formula to determine the change in temperature of the two fluids:
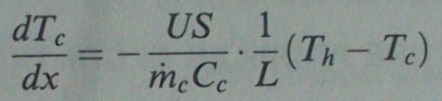
Is there any option how I can determine the change in temperature when I do have the crosssectional geometry, heat transfer coefficients and the bulk fluid temperatures, but not the entire surface area of the exchanger?
Thank you already for your help!
I just found that I made a horrible mistake in my calcualion for a phase chaning heat exchanger desing. For the design i wanted to include the change in physical properties, for which I decided to create the heat exchanger in a discretized manner. I did this and calculated the heat transfer coefficient on each side, which was no problem. but depending on the step size I chose, the entire length of the heat exchanger varies, since the formula for the overall heat transfer coefficient apparently can only be used on the total length of the exchanger, which is of course not possible since it is unknown.
The formula I used for the overal heat transfer coefficient is the following:
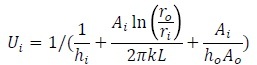
The areas Ai and Ao I calculated are of course in the discrete way of my design a function of the stepsize dx. With this the overall heat transfer coefficient changes strongly with stepsize, leading to a different length of the overall exchanger (I fixed a required output temperature, based on the saturation temperature of one of the fluids).
Now I dont know how I can calculate the change in heat of the fluids. Before I was using the following formula to determine the change in temperature of the two fluids:
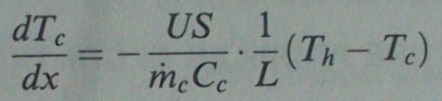
Is there any option how I can determine the change in temperature when I do have the crosssectional geometry, heat transfer coefficients and the bulk fluid temperatures, but not the entire surface area of the exchanger?
Thank you already for your help!
