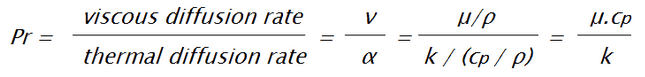-
1
- #1
Jgrovdal
Electrical
- May 6, 2022
- 2
Hi
I am currently trying to calculate the temperature a conductor will reach when applying 50 amps to it. The conductor is an 16mm^2 copper stranded wire. The length is 2m. I am trying to make a model in Matlab to calculate it, is it possible to make it that way? Or is there a better way?
The model I am trying to use is the one from this paper:
But it has not been successful yet.
My problem seems to be that there still is some variables that is missing and therefore my calculations don't give me a result. For now I miss the Prandtl number and can't continue.
The variables I have found:
L = 2; %Length
I = 50; %Current
R_ref = 5.54830155*1^-4; %Reference resistance
alfa_T = 0.00393; %Resistance at temperature rise
T_ref = 21; %Reference temperature for Resistance
r_c = 1/2*12.1*10^-3; %Radius core
r_i = 1/2*15.45*10^-3 ; %Radius whole
g = 9.81; %Gravitation
l_alfa = 2*r_i; %Characteristics of the length of structure
sigma = 5.6704*10^-8; %Stefan Boltzmann constant
epsilon = 0.95; %Assumed after an paper
rho = 3.19*10^-8; %Ohm per meter
pi = 3.14; %Pie
lambda_c = 386; %Thermal conductivity conductor
c_c = 3.4*10^6; %Specific heat capacities conductor
c_i = 2.245*10^6; %Specific heat capacities isolation
lambda_i = 0.21; %Thermal conductivity conductor
M = 5; %Parameter - Gaver-Stehfest-algorithm (Dimensionless)
T_E = 25; %Temperature ambient
T_EK = T_E+273.1;
T_S = 25; %Temperature surface
T_SK = T_S+273.1;
T_0 = 21; %Reference temperature
beta = 1/T_EK; %Coefficient of thermal expansion
lambda_air = 25.90; %Thermal conductivity Air maybe 0.0246
Thanks in advance
I am currently trying to calculate the temperature a conductor will reach when applying 50 amps to it. The conductor is an 16mm^2 copper stranded wire. The length is 2m. I am trying to make a model in Matlab to calculate it, is it possible to make it that way? Or is there a better way?
The model I am trying to use is the one from this paper:
But it has not been successful yet.
My problem seems to be that there still is some variables that is missing and therefore my calculations don't give me a result. For now I miss the Prandtl number and can't continue.
The variables I have found:
L = 2; %Length
I = 50; %Current
R_ref = 5.54830155*1^-4; %Reference resistance
alfa_T = 0.00393; %Resistance at temperature rise
T_ref = 21; %Reference temperature for Resistance
r_c = 1/2*12.1*10^-3; %Radius core
r_i = 1/2*15.45*10^-3 ; %Radius whole
g = 9.81; %Gravitation
l_alfa = 2*r_i; %Characteristics of the length of structure
sigma = 5.6704*10^-8; %Stefan Boltzmann constant
epsilon = 0.95; %Assumed after an paper
rho = 3.19*10^-8; %Ohm per meter
pi = 3.14; %Pie
lambda_c = 386; %Thermal conductivity conductor
c_c = 3.4*10^6; %Specific heat capacities conductor
c_i = 2.245*10^6; %Specific heat capacities isolation
lambda_i = 0.21; %Thermal conductivity conductor
M = 5; %Parameter - Gaver-Stehfest-algorithm (Dimensionless)
T_E = 25; %Temperature ambient
T_EK = T_E+273.1;
T_S = 25; %Temperature surface
T_SK = T_S+273.1;
T_0 = 21; %Reference temperature
beta = 1/T_EK; %Coefficient of thermal expansion
lambda_air = 25.90; %Thermal conductivity Air maybe 0.0246
Thanks in advance