Greetings from Brazil,
I am trying to build a spreadsheet to estimate how cold a fluid would be at the end of a pipe.
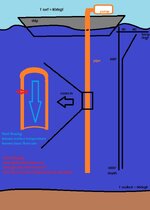
This non-insulated steel pipe (let`s say ~3000ft long), would be vertical in the sea, from surface to sea bed. At surface a pump would pump down, with a certain constant flow rate.
This is out of my expertise, so I`d like to have some guidance from the community.
Initial doubts, on how to work it (but please advise):
1. I am thinking about dividing this 3000ft long pipe into ten 300ft sections. So I`d solve them separately in a sequence, from top to bottom. Each 300ft section would have a constant sea temperature along it, for simplification.
2. Sea water gradient goes from ~80degF at surface to ~40degF at ~600ft, where it would remain, at least for simplification, at a constant temperature of 40degF until the sea bed.
3. I don`t know how to treat the sea here. I`d like to assume it never heats up (even very close to the pipe) for simplification. I think I could say it is a constant heat (cold) source. Please advice.
4. Because of friction, fluid would generate heat as it flows down (I`d be pumping sea water, for simplification, if any).
Doubts on how to iterate it:
T=to
static conditions before start pumping down
T=t1
1. solve the first 300ft section
- assume fluid enters this section at 80degF and after moving the entire 300ft, the final temperature is the heat generated by friction plus initial temperature minus heat lost to the pipe which is at sea temperature
2. do the same for all other 9 sections, using for each section the average sea temperature at depth as the initial temperature
- after all 9 sections have been calculated, this is the end of iteration 1 (end of T=t1)
T=t2
1. again, solve first 300ft section
- here I am lost, as fluid enters the top of the first section with the same temperature from surface (80degF), but how do I take into consideration the exit temperature already calculated on the previous iteration? If i don`t, this temperature will never change and I think the iteration converges and freezes.
2. solve the second 300ft section (and repeat for the other sections)
- initial temperature for each section is the exit temperature of first section at T=t1
Please advise the formulas to be used. I was reading INCROPERA chapter 8 about internal flow and think that maybe the constant surface temperature approach could work.
Thanks,
Igor
I am trying to build a spreadsheet to estimate how cold a fluid would be at the end of a pipe.
This non-insulated steel pipe (let`s say ~3000ft long), would be vertical in the sea, from surface to sea bed. At surface a pump would pump down, with a certain constant flow rate.
This is out of my expertise, so I`d like to have some guidance from the community.
Initial doubts, on how to work it (but please advise):
1. I am thinking about dividing this 3000ft long pipe into ten 300ft sections. So I`d solve them separately in a sequence, from top to bottom. Each 300ft section would have a constant sea temperature along it, for simplification.
2. Sea water gradient goes from ~80degF at surface to ~40degF at ~600ft, where it would remain, at least for simplification, at a constant temperature of 40degF until the sea bed.
3. I don`t know how to treat the sea here. I`d like to assume it never heats up (even very close to the pipe) for simplification. I think I could say it is a constant heat (cold) source. Please advice.
4. Because of friction, fluid would generate heat as it flows down (I`d be pumping sea water, for simplification, if any).
Doubts on how to iterate it:
T=to
static conditions before start pumping down
T=t1
1. solve the first 300ft section
- assume fluid enters this section at 80degF and after moving the entire 300ft, the final temperature is the heat generated by friction plus initial temperature minus heat lost to the pipe which is at sea temperature
2. do the same for all other 9 sections, using for each section the average sea temperature at depth as the initial temperature
- after all 9 sections have been calculated, this is the end of iteration 1 (end of T=t1)
T=t2
1. again, solve first 300ft section
- here I am lost, as fluid enters the top of the first section with the same temperature from surface (80degF), but how do I take into consideration the exit temperature already calculated on the previous iteration? If i don`t, this temperature will never change and I think the iteration converges and freezes.
2. solve the second 300ft section (and repeat for the other sections)
- initial temperature for each section is the exit temperature of first section at T=t1
Please advise the formulas to be used. I was reading INCROPERA chapter 8 about internal flow and think that maybe the constant surface temperature approach could work.
Thanks,
Igor