Burner2k
Aerospace
- Jun 13, 2015
- 193
Hello,
I am looking to some help (references) about verification of FEA methodology.
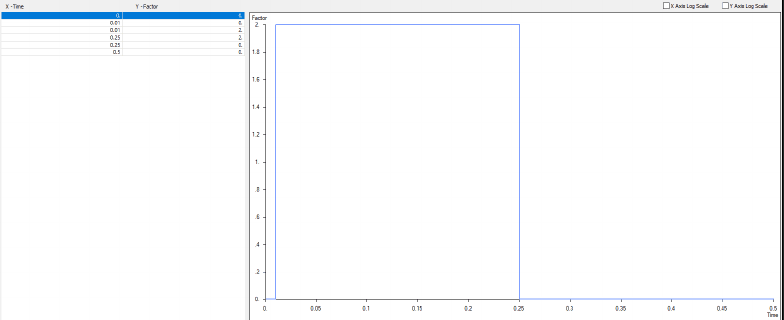
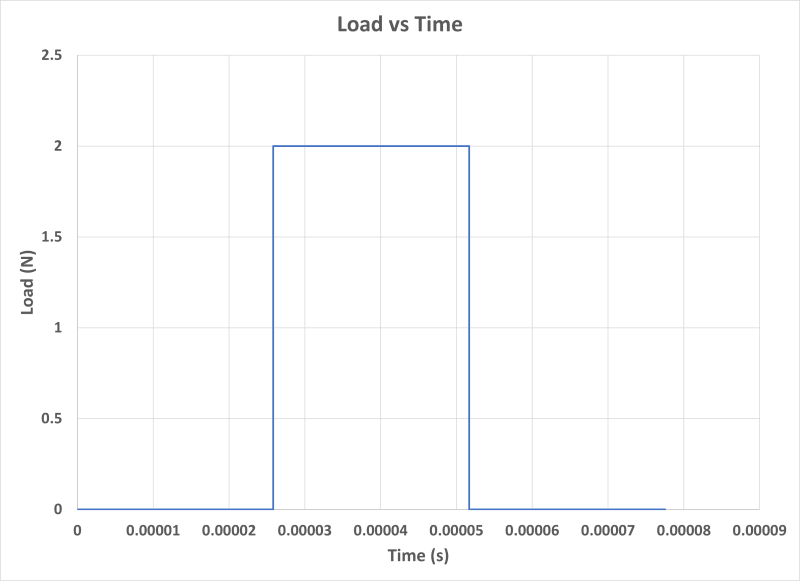
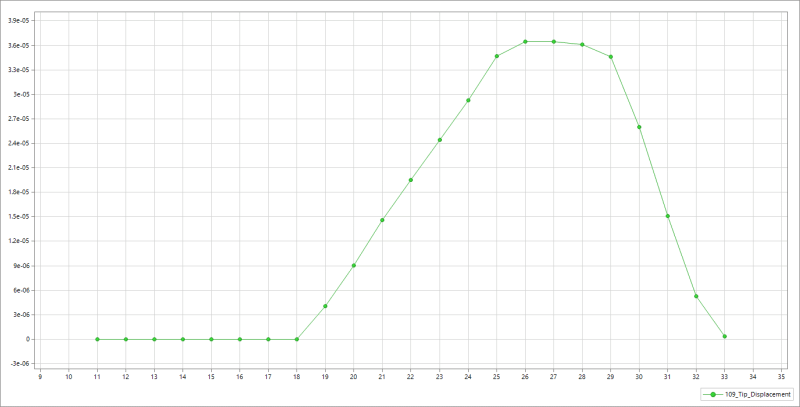
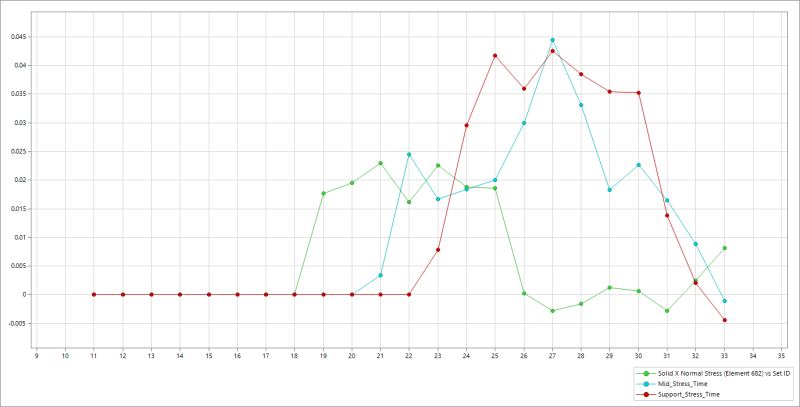
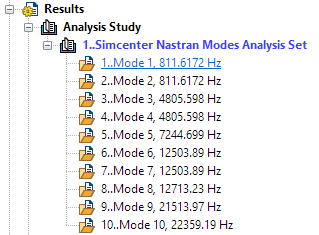
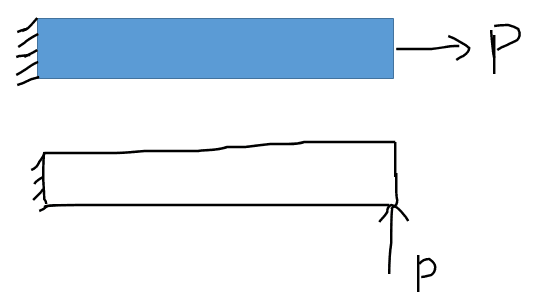
Specifically for transient dynamic analysis. I am thinking of a simple tensile load or pointed transverse load
on cantilever as shown below. I will first try with axial since it will be a single DOF system & hence easier to do hand calcs.
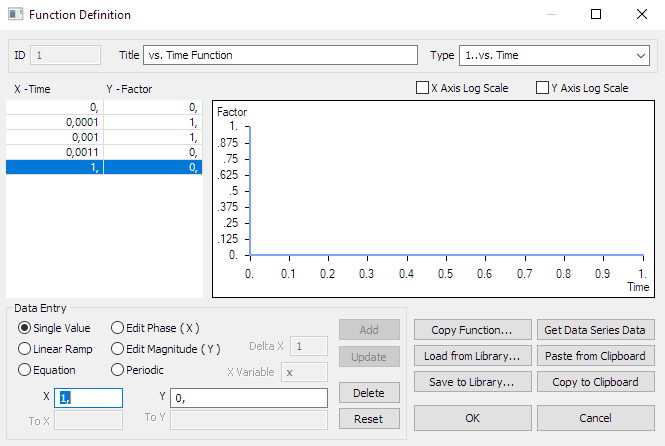
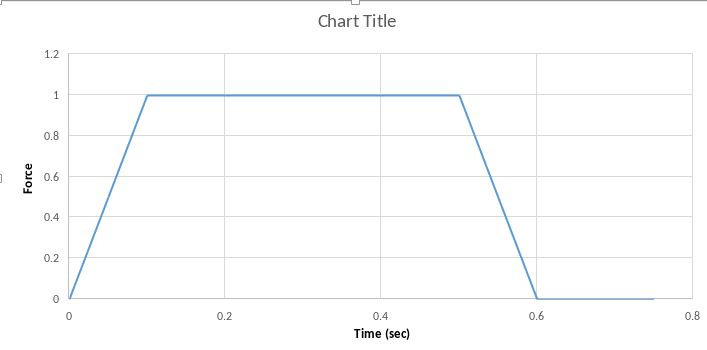
The force will be a function of time as shown below.
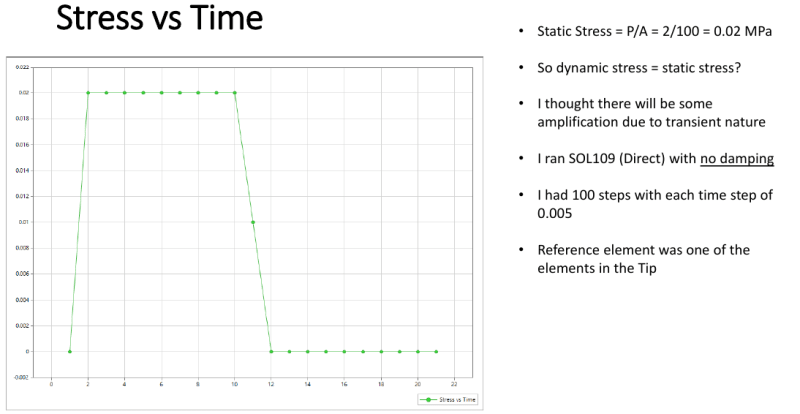
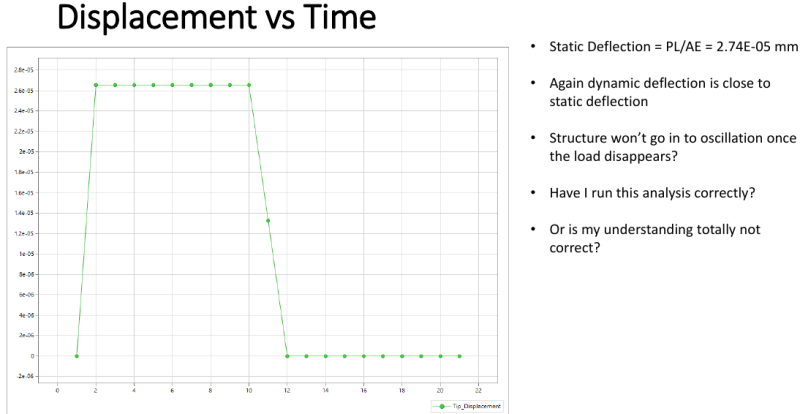
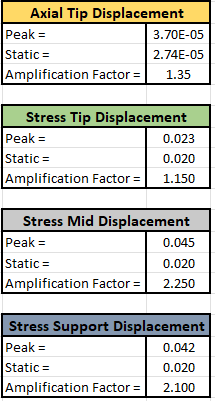
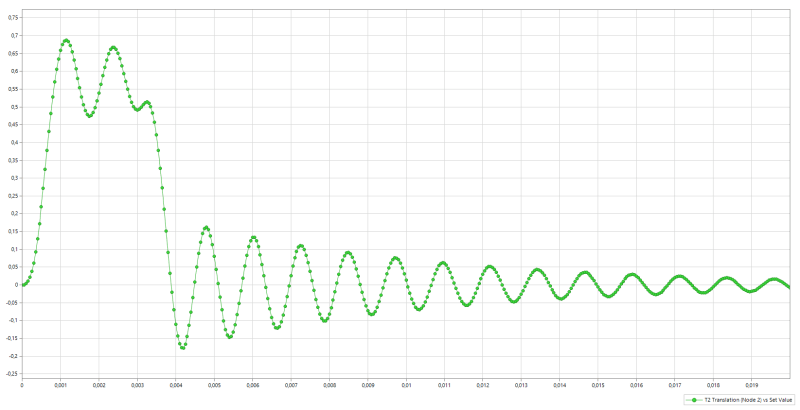
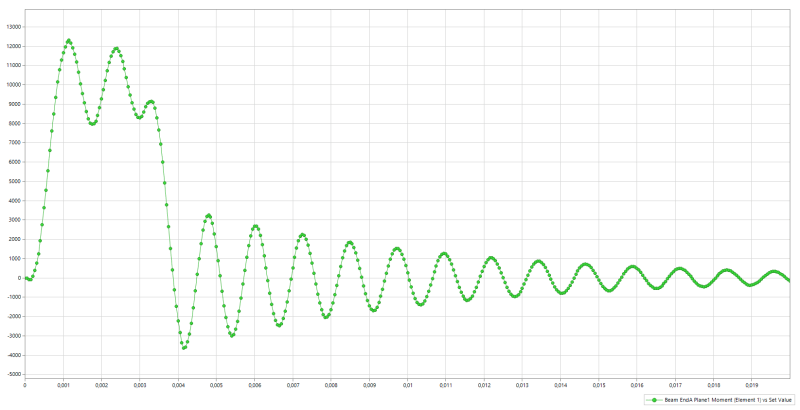
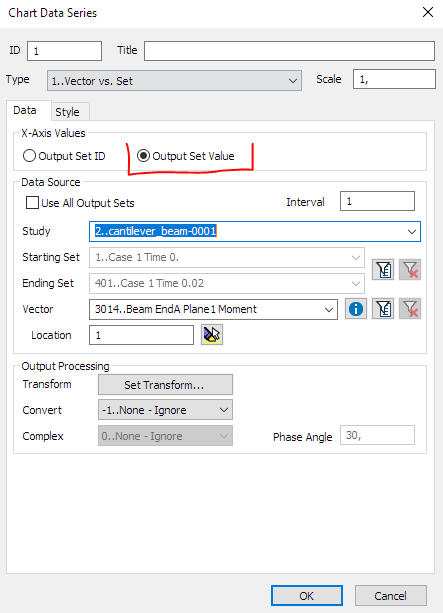
I am hoping to correlate FEA output with hand calculations. I am not sure if hand calculations can be even
performed for the above. If yes, I would appreciate some help on where I can find relevant formulas. Basic idea is to figure out I've got the methodology right.
I am looking to some help (references) about verification of FEA methodology.
Specifically for transient dynamic analysis. I am thinking of a simple tensile load or pointed transverse load
on cantilever as shown below. I will first try with axial since it will be a single DOF system & hence easier to do hand calcs.

The force will be a function of time as shown below.

I am hoping to correlate FEA output with hand calculations. I am not sure if hand calculations can be even
performed for the above. If yes, I would appreciate some help on where I can find relevant formulas. Basic idea is to figure out I've got the methodology right.