Hello Everyone,
I am a person whom only just got an engineering position and I am having a bit of trouble in a project.
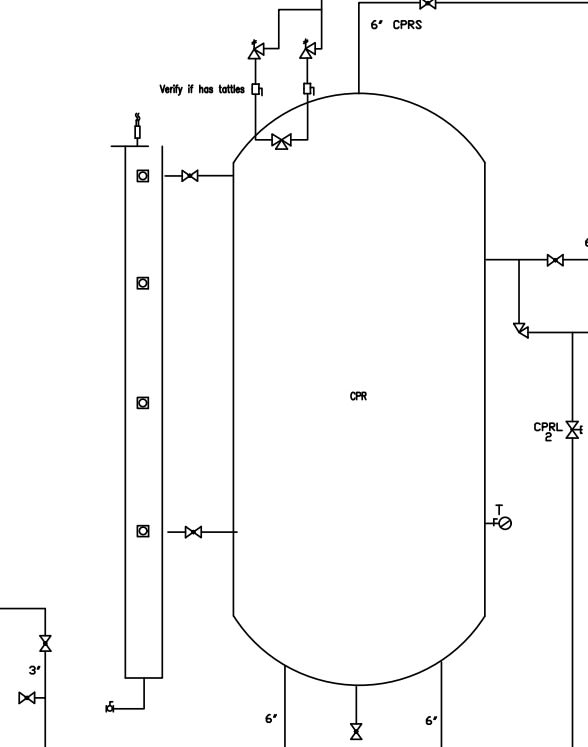
You see, one of the pumps in our refrigeration system is suffering cavitation issues and I am attempting to determine the NPSHa to it. To make a long story short, one of the calculations for this involves the height of the fluid in the Control Pressure Receiver tank located above the pump. This tank is a closed off pressurized vertical cylindrical tank with Ellipsoidal concaved ends.
Now, I have already calculated the total volume capacity of the tank using the equations below and attached.
Vbottomend= (Π/6)*(((3/0.5)*ID*(H^2)) -(2/(0.5^2))*H^3))
Vtopend= (π/12)*((3*(ID^2)*H)-((4/(0.5^2))*(H^3))
Vcylinder=(π*((ID^2)/4)*CL)
Where:
ID=Inner diameter (m)
CL=Height of cylindrical section with the continuous cross section (m)
H= Height of liquid itself (m)
For determining the total volume capacity, I substituted the value of "H" with the Tank Head internal depth (IDD).
And we have a program to measure and keep track the percent volume within the tank.
Now, my dilemma is this. I cannot determine any means to calculate the height of the fluid in the tank based on the percent volume. One equation which was shown to me (Height = Total height * (percent volume/total volume) only applied to tanks which were cylindrical with flat ends.
Do any of you know of any solution?
I already tried the method of adding the equations together and solving for H, only for the resulting equation to be a complete mess.
I am a person whom only just got an engineering position and I am having a bit of trouble in a project.
You see, one of the pumps in our refrigeration system is suffering cavitation issues and I am attempting to determine the NPSHa to it. To make a long story short, one of the calculations for this involves the height of the fluid in the Control Pressure Receiver tank located above the pump. This tank is a closed off pressurized vertical cylindrical tank with Ellipsoidal concaved ends.
Now, I have already calculated the total volume capacity of the tank using the equations below and attached.
Vbottomend= (Π/6)*(((3/0.5)*ID*(H^2)) -(2/(0.5^2))*H^3))
Vtopend= (π/12)*((3*(ID^2)*H)-((4/(0.5^2))*(H^3))
Vcylinder=(π*((ID^2)/4)*CL)
Where:
ID=Inner diameter (m)
CL=Height of cylindrical section with the continuous cross section (m)
H= Height of liquid itself (m)
For determining the total volume capacity, I substituted the value of "H" with the Tank Head internal depth (IDD).
And we have a program to measure and keep track the percent volume within the tank.
Now, my dilemma is this. I cannot determine any means to calculate the height of the fluid in the tank based on the percent volume. One equation which was shown to me (Height = Total height * (percent volume/total volume) only applied to tanks which were cylindrical with flat ends.
Do any of you know of any solution?
I already tried the method of adding the equations together and solving for H, only for the resulting equation to be a complete mess.