Help with Planetary Gear Arrangement

[msb101]

Hi all,

Need help with a Gear Train described below. A rough sketch is attached.

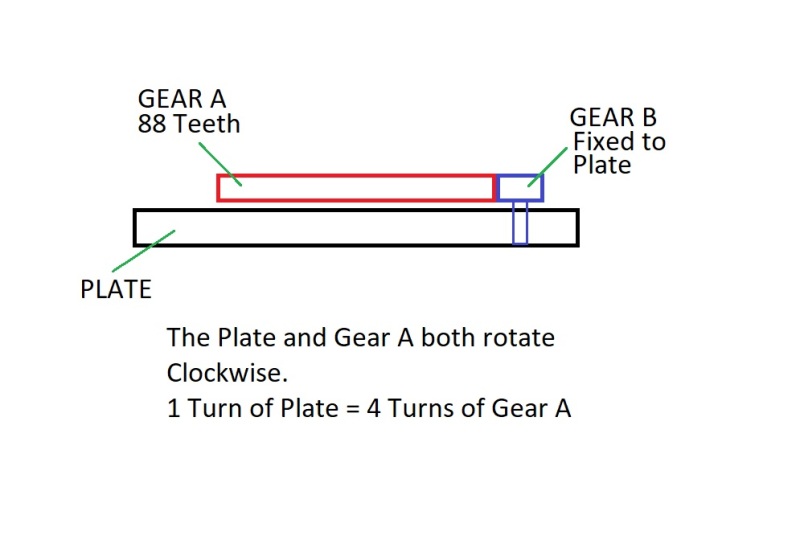
1)We have a Round Plate above which there is a 88 Teeth Gear (Gear A). Both have their own drive and the ratio is 1:4. For every 1 turn of the plate, the Gear A rotates 4 times. They both rotate in the same clockwise direction.

2)On the plate is mounted a Gear B which meshes with the 88 Tooth Gear A.

I want it such that for every 1 rotation of the Plate, the Gear B rotates 18 times.

I am unable to figure out the no. of Teeth for Gear B, and would be grateful for any help with the formula/calculation.
If required, I can change the ratio between the Plate and the Gear A and/or the No. of Teeth on Gear A.

 

[drawoh]

msb101,

That's not really a planetary gear system.

If gear[ ]B rotates 18[ ]times for each rotation of the plate, it rotates 18/4[ ]times for each rotation of gear[ ]A. You need 88teeth/18[×]4=19.6teeth, approximately. It will rotate in the opposite direction. If you want to turn exactly 18[ ]times per turn of the plate, you need gears with 90[ ]teeth and 20[ ]teeth, respectively.

This is not very complicated.

--
JHG

 

[msb101]

Hi,

Thanks for your reply. We did a simulation in solidworks with the 90-20 Teeth Combination and it didn't work. The number of rotations of Gear B don't remain constant with every rotation of the plate.

 

[drawoh]

msb101,

If you have a gear train of any kind with round gears in constant mesh, the output gear should rotate at a constant rate. If your output is varying, something else is moving.

--
JHG

 

[msb101]

We did a simple simulation in solidworks and everything is fixed, so nothing else is moving.
It gives us approx. 13.5 revolutions

 

[msb101]

Hi,

What worked is 90-15 combination. It gives us exact 18. Thanks.

 

[spigor]

Your description leads to believe, that the revolutions of the gear B are measured relative to same thing as the revolutions of the plate, e.g. a housing in which all the items rotate. The combination 90-15 is correct relative to the plate, i.e. for every one revolution of the plate relative to the housing the gear B makes 18 revolutions relative to the plate, and 17 revolutions relative to the housing.