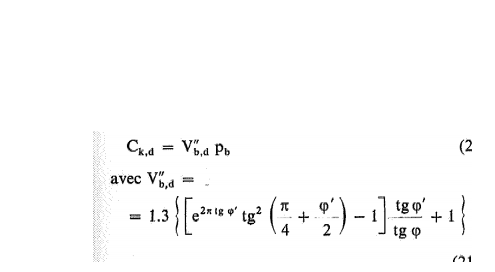Hi,
I have an equation which is shown below, which says qc (cone resistance) = .....
Now i need to calculate the effective angle of internal friction from the below formula. So i need to make a new formula
which starts with φ'= ......
qc= 1.3 × exp[2π tanφ'] × tan2[(π/4)+ fracφ'2] × σv0
And i have no idea what is this fracφ'2.
I am stuck with this value.
I cannot use any other formula to calculate φ'. It is that i have to use this formula./
Does anyone know how to reverse the equation so that i can calculate effective angle of internal friction?
The qc value and effective stress are given.
I have an equation which is shown below, which says qc (cone resistance) = .....
Now i need to calculate the effective angle of internal friction from the below formula. So i need to make a new formula
which starts with φ'= ......
qc= 1.3 × exp[2π tanφ'] × tan2[(π/4)+ fracφ'2] × σv0
And i have no idea what is this fracφ'2.
I am stuck with this value.
I cannot use any other formula to calculate φ'. It is that i have to use this formula./
Does anyone know how to reverse the equation so that i can calculate effective angle of internal friction?
The qc value and effective stress are given.