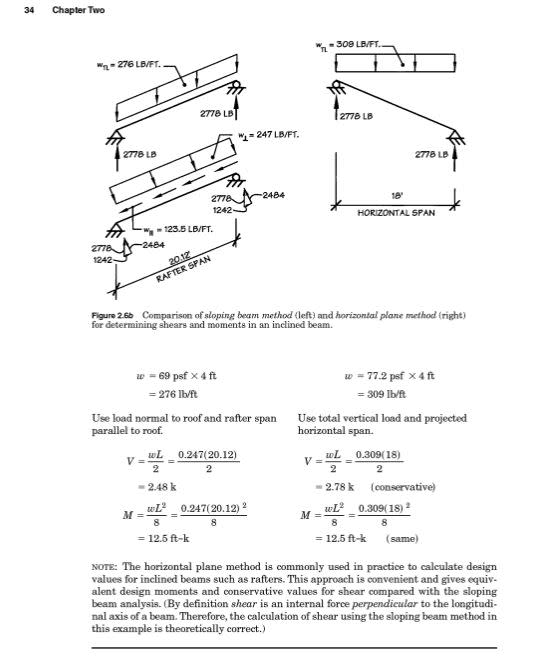
Ok, lets say you have a rafter which is 3m long in plan and inclined at a 40 degree angle, how do you account for the incline. I normal adjust the loading, say 1KN/m by dividing by cos(40) so 1/(cos40) = 1.31 KN/m and then design it. However, would it be better to adjust the length instead of the loading. So dividing 3/cos(40) to give you 3.92m in length.
This makes a bit of difference when working with timber and trying to calculate deflection. Would be really grateful if I could hear your opinions. Thanks
This makes a bit of difference when working with timber and trying to calculate deflection. Would be really grateful if I could hear your opinions. Thanks