canadiancastor
Structural
- Apr 13, 2014
- 36
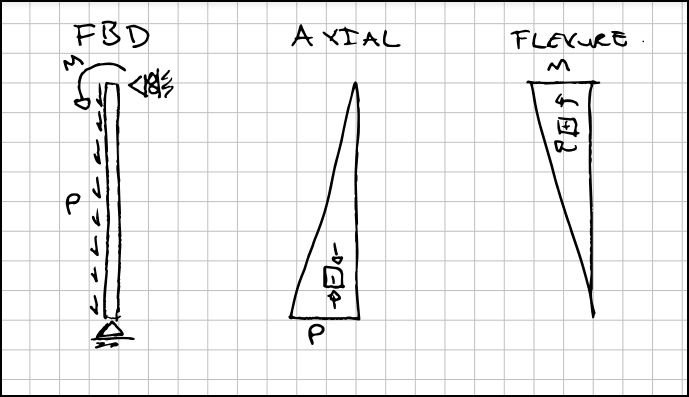
I'm looking at setting up calculations for steel angles (according to CSA S16-19) that will take into consideration any compression, flexion or combination of the two. I don't have a problem with calculating the section strengths, but I'm a bit confused with what I should take for maximum loading. Say I have a complex beam that has positive and negative moments (strong AND weak axis) and positive and negative axial load (probably impossible in practice, but I want to code this only once).
Question #1: Would it be allowed to run calculations section by section, that is find flexural and axial loads (Mfx, Mfy, Cf) at each point along the beam and compute strength and interaction checks? What seems to be breaking my brain with this approach is that everything we calculate in the standard is for "beam" loading, and not "section" loading or stress. If this is allowed, are there any limits? Could it be imagined that I have huge flexure on one end, huge axial on the other end, and basically no "actual" interaction between both sides?
Question #2: If we are not allowed to run calculations section by section as discussed above, as I suspect, that means we need to find the maximum and minimum values of all of the loading before we start our calculation checks. Since my beam in not symmetric, this would mean getting max(Mfx), min(Mfx), max(Mfy), min(Mfy), max(Cf), min(Cf) and checking all of those against their corresponding strengths. Then for interaction, I would have to permute all of these, so for the flexural / compression interaction, that would mean that I would have 8 cases per load combination to check:
max(Mfx)/Mrx+, max(Mfy)/Mry+, max(Cf)/Tr+
max(Mfx)/Mrx+, max(Mfy)/Mry+, min(Cf)/Cr-
max(Mfx)/Mrx+, min(Mfy)/Mry-, max(Cf)/Tr+
max(Mfx)/Mrx+, min(Mfy)/Mry-, min(Cf)/Cr-
min(Mfx)/Mrx-, min(Mfy)/Mry-, max(Cf)/Tr+
min(Mfx)/Mrx-, min(Mfy)/Mry-, min(Cf)/Cr-
min(Mfx)/Mrx-, max(Mfy)/Mry+, max(Cf)/Tr+
min(Mfx)/Mrx-, max(Mfy)/Mry+, min(Cf)/Cr-
Seems like there should be a simpler (albeit probably conservative) way to find the worst case? I guess if I could discard all of the cases where a "max" is negative or a "min" is positive? Any other ideas?
Question #1: Would it be allowed to run calculations section by section, that is find flexural and axial loads (Mfx, Mfy, Cf) at each point along the beam and compute strength and interaction checks? What seems to be breaking my brain with this approach is that everything we calculate in the standard is for "beam" loading, and not "section" loading or stress. If this is allowed, are there any limits? Could it be imagined that I have huge flexure on one end, huge axial on the other end, and basically no "actual" interaction between both sides?
Question #2: If we are not allowed to run calculations section by section as discussed above, as I suspect, that means we need to find the maximum and minimum values of all of the loading before we start our calculation checks. Since my beam in not symmetric, this would mean getting max(Mfx), min(Mfx), max(Mfy), min(Mfy), max(Cf), min(Cf) and checking all of those against their corresponding strengths. Then for interaction, I would have to permute all of these, so for the flexural / compression interaction, that would mean that I would have 8 cases per load combination to check:
max(Mfx)/Mrx+, max(Mfy)/Mry+, max(Cf)/Tr+
max(Mfx)/Mrx+, max(Mfy)/Mry+, min(Cf)/Cr-
max(Mfx)/Mrx+, min(Mfy)/Mry-, max(Cf)/Tr+
max(Mfx)/Mrx+, min(Mfy)/Mry-, min(Cf)/Cr-
min(Mfx)/Mrx-, min(Mfy)/Mry-, max(Cf)/Tr+
min(Mfx)/Mrx-, min(Mfy)/Mry-, min(Cf)/Cr-
min(Mfx)/Mrx-, max(Mfy)/Mry+, max(Cf)/Tr+
min(Mfx)/Mrx-, max(Mfy)/Mry+, min(Cf)/Cr-
Seems like there should be a simpler (albeit probably conservative) way to find the worst case? I guess if I could discard all of the cases where a "max" is negative or a "min" is positive? Any other ideas?