GoncaloPT
Structural
- Jun 9, 2020
- 24
Hi! Hope you all are doing great 
I'm in need of some tips/help regarding some forces for the design of a structure.
I have a sliding window that will impact on a steel square profile (represented in blue). The glazing sliding window will have a total mass around 150 kg, a impact height of around 2 meters.
Assuming a terminal velocity of 0.2 m/s (vf) what should be the impact load expected on the steel structure? Can anyone provide some guidelines on how to estimate this loads?
I understand this should also consider a collision distance and a impact duration, but i have no ideia of what are reasonable values for these.
Any input would be much appreciated
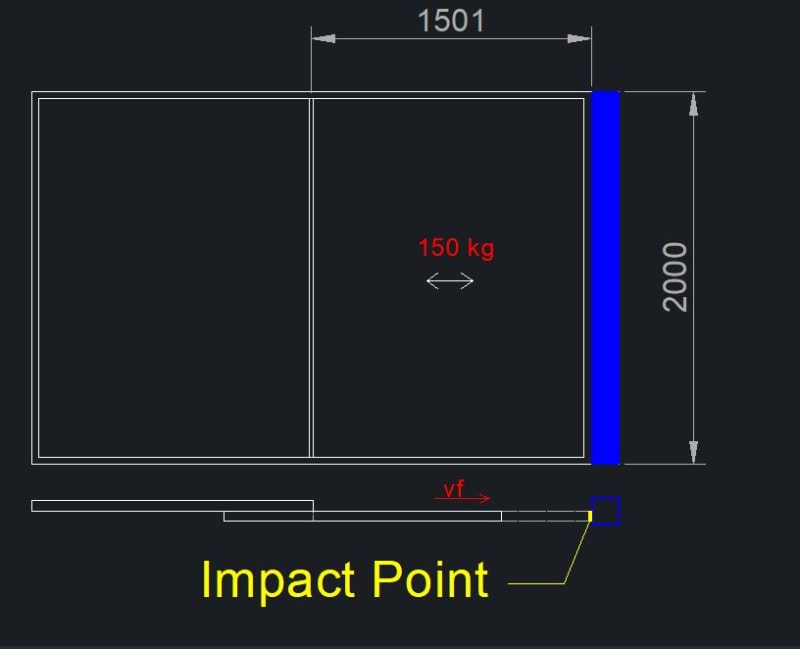
I'm in need of some tips/help regarding some forces for the design of a structure.
I have a sliding window that will impact on a steel square profile (represented in blue). The glazing sliding window will have a total mass around 150 kg, a impact height of around 2 meters.
Assuming a terminal velocity of 0.2 m/s (vf) what should be the impact load expected on the steel structure? Can anyone provide some guidelines on how to estimate this loads?
I understand this should also consider a collision distance and a impact duration, but i have no ideia of what are reasonable values for these.
Any input would be much appreciated