Impact Force on Steel Member Frame AS3774 vs. Kinetic Energy Method

[Jhinnie2]

Hi All,

I know there's a lot of threads on impact loads but honestly I'm still confused as there's so many different answers. I have a bolted frame with 360UBs and 230 PFCs, and essentially there are multiple 300kg counterweights in a row which each have a rod running through. Designing for if the chain holding the counter weight fails (which it has failed in the past), these two beams will catch the counterweight with the rod hitting simulatenously so load split 50/50 (ie. to stop it falling into a chute below and damaging the platework). The fall height is 0.4 metres. Based on this V= 2gh = 2.8 m/s.

Looking at two methods here 1. AS3774 Impact loads on hoppers due to dumping, they estimate either 0.1 or 0.3 x (mass x V ) which gives an impact of around 90 to 252 kN total which seems quite high in magnitude? Notabely the counterweight is quite small and compact solid steel.

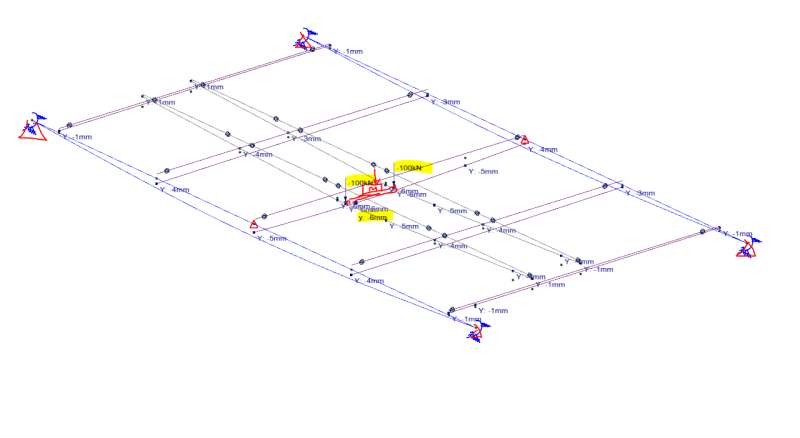
2. method is the kinetic energy = potential energy for the elastic beam. So P = delta x mass x V^2 and for this method I apply a unit load of 100 kN on each of the two beams, and I have moved these loads along the length of the beam to find the worst case scenario to design my frame. Say for example I get 6 mm deflection underneath each beam for these two loads (shown in screenshot), how do I got about back calculating the real world impact force that I should design frame for the impact load case? If delta is 6mm and P is 100 kN, then k = P/delta = 16,667 kN/m. Then how do I back calculate what P is in kN from the 250kg counterweight dropped from 0.4 m above beams?

Thanks

 

[Settingsun]

For method 2, the potential energy is W*(H+δ). The energy absorbed is Σ(P*δ/2). Equate those to get P.

Edit: that's the basic theory but, having done the numbers, you'd have to look at inertia and dynamic analysis for your case.

 

[human909]

Do not use AS3774. It is not at all appropriate for this scenario. You cannot compare the dropping of steel on steel to rules of thumb for loose bulk materials. Furthermore you really need to go much deeper than you already have and properly understand the problem. Is this a frame sole to catch these counterweights? In which case you are massively overdesigning. Why not just have a loose catch strap with a suitable energy absorber? Or just a nice lightweight catch frame that will deflect suitably.

Working out the impact energy from the beam deflection as steveh49 said is suitable approach if your assumptions are correct. And while I could very much be mistaken, based on your figures there you are looking at ~400kN based on your input values. Eg 0.4m x 6kN = 2.4kJ === 400kN x 0.012m *1/2 = 2.4kJ

However:

for this method I apply a unit load of 100 kN on each of the two beams, and I have moved these loads along the length of the beam to find the worst case scenario to design my frame. Say for example I get 6 mm deflection underneath each beam for these two loads

No. You seemed to have found the LEAST worst case scenario. The highest deflection point is the least stiff point and will absorb the most energy. The worst case scenario is right near your fixities where you'll find that the deflection decreases and the impact force increases with no bounds start too consider plastic analysis.

Of course we haven't event considered the flooring or whatever is constraining your counterweights.

 

[Jhinnie2]

frame sole to catch these counterweights? In which case you are massively overdesigning. Why not just have a loose catch strap with a suitable energy absorber? Or just a nice lightweight catch frame that will deflect suitably.

The client basically wants this frame to be stiff as it supports grating and need this area to be accessed. We suggested a mechanical solution with springs to reduce the impact but they just want a 'structural' solution with more mass thrown at it so basically a big overdesign. How about this approach?

 

[WARose]

That looks kind of like Blodgett's solution (in 'Design of Welded Structures'). Which is what I have typically used. However for a complex frame you may have to figure a equivalent system or maybe the software can do it based on a ramp load input. (I know STAAD can.)

[red]EDIT:[/red] I tell you the thing I have never been too certain on is if a load/impact factor should be used in addition to Blodgett's method. You look at it, and it really doesn't take into account the dynamics of the system.

 

[human909]

I haven't checked your figures nor have I used that approach but those results don't seem unreasonable for direct impact along the beam with your other assumptions. If you have grating over the beam it will reduce the peak values considerably as it deforms.

 

[Settingsun]

I believe that the impact factor is just your original method #2 rearranged (equating potential energy to internal work). I made a mistake when I did the numbers first time and got an unreasonable number, which is why I thought there would be more at play.

PS: Re-check the 52.6 impact factor in your calc.