nivoo_boss
Structural
Hey everyone!
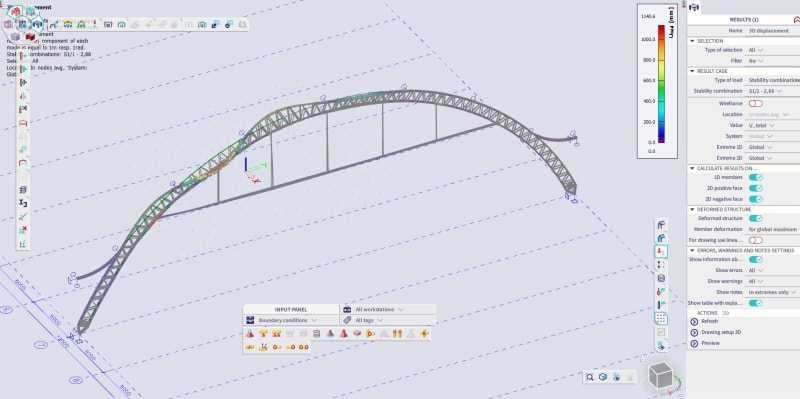
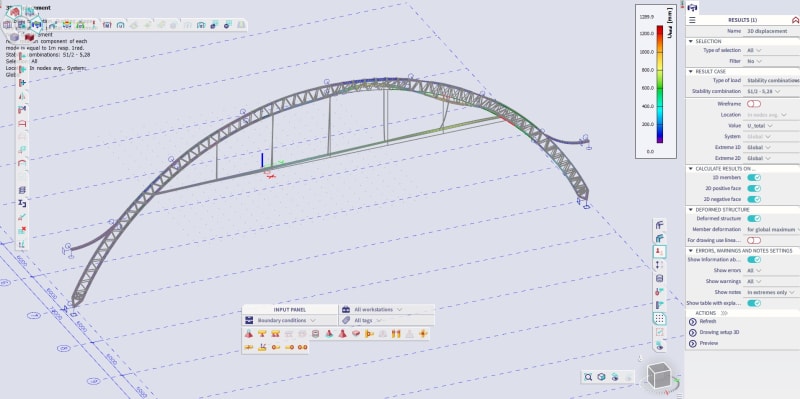
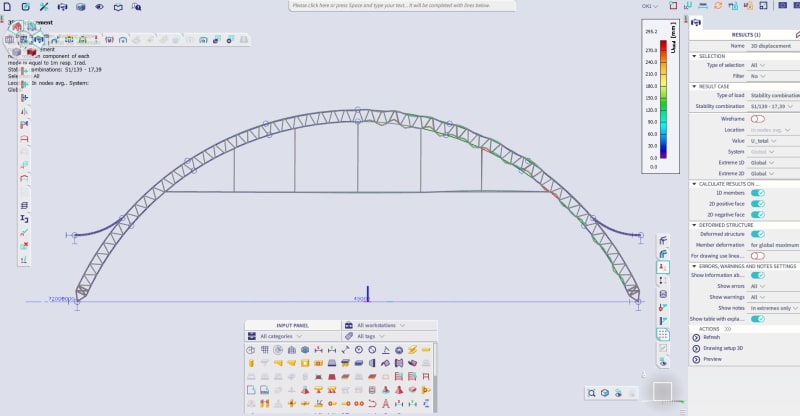
Perhaps you can give some advice on how to check if this steel arc will buckle under the specified ULS load. It's created in SCIA Engineer software. It has a span of 45 m. It's like a 1 m high steel truss with U-sections for chords and L-sections for brace members.
If you can point me to some hand calculation methods for this analysis, I would be grateful as well. But perhaps you can give me some advice on how to approach it in software? I can make stability combinations in SCIA and then it calculates me any amount of buckling modes I specify with a factor alpha_cr after them - basically it should mean that the structure will buckle under my load factored by that alpha critical factor.
A picture from my calculation model:
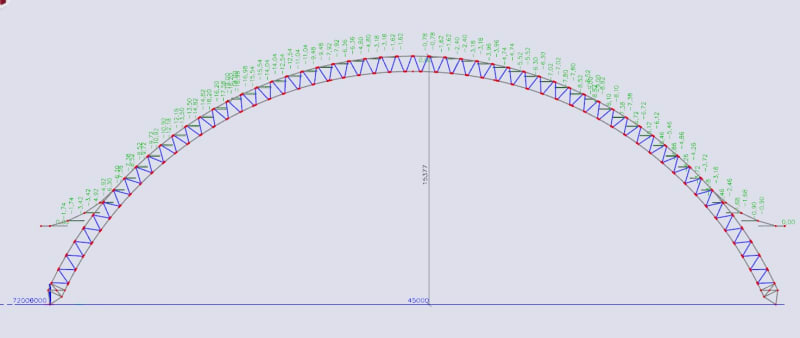
Perhaps you can give some advice on how to check if this steel arc will buckle under the specified ULS load. It's created in SCIA Engineer software. It has a span of 45 m. It's like a 1 m high steel truss with U-sections for chords and L-sections for brace members.
If you can point me to some hand calculation methods for this analysis, I would be grateful as well. But perhaps you can give me some advice on how to approach it in software? I can make stability combinations in SCIA and then it calculates me any amount of buckling modes I specify with a factor alpha_cr after them - basically it should mean that the structure will buckle under my load factored by that alpha critical factor.
A picture from my calculation model: