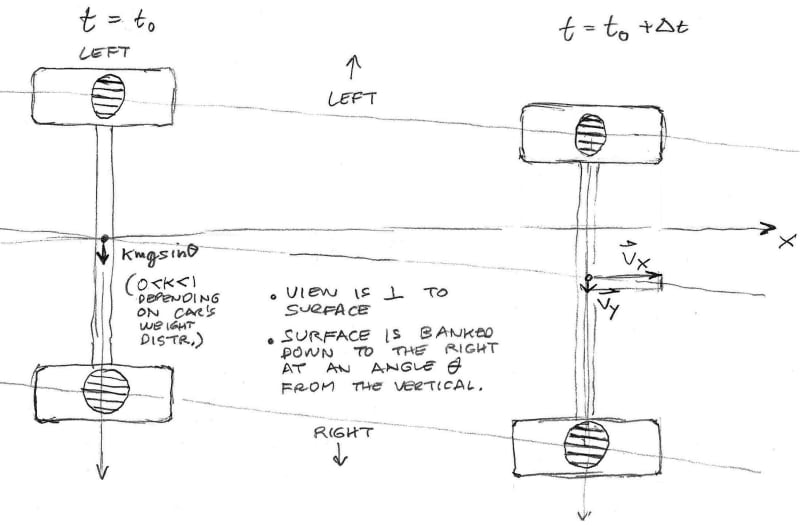
Hi Cibachrome - All of that makes sense. My hypothetical axle is in static equilibrium after the steady state is attained, so the external moments and forces must sum to zero. The initiation of the transient state as I've described it could be created by having the vehicle's COM height go from zero to whatever might be its nominal value for t > t naught.
Some assumptions about this axle: No differential. No roll steer. No assumptions whatsoever about its suspension aside from ensuring the conditions shown in my sketch are met. Identical tires left and right. So, this axle doesn't exist in real life, just as massless rods with infinite rigidity, which are cited everywhere in physics discourses, don't exist either. Even so, I think considering what happens to this axle has valid real-world implications.
Here's my understanding of what's going on here:
We know for t> t naught that the forces and the moments change. The lower tire becomes more heavily loaded than the higher one. The lateral force from the lower tire is greater than from the higher tire. Without considering pneumatic trail for the time being, the slip angle for the lower tire *must* be (please correct me if I'm wrong) greater than for the higher tire.
We know this divergence in slip (and therefore tire contact patch velocities) can't continue indefinitely, or the axle will separate, or the higher tire will start to slide.
So at some time after t = t naught, static equilibrium is attained, the tire velocities restore to parallelism (probably exponentially over time), and the slip angles become equal. Regarding pneumatic trails, we assign to our imaginary suspension the additional task of creating an equal and opposite Mz to maintain zero yaw acceleration.
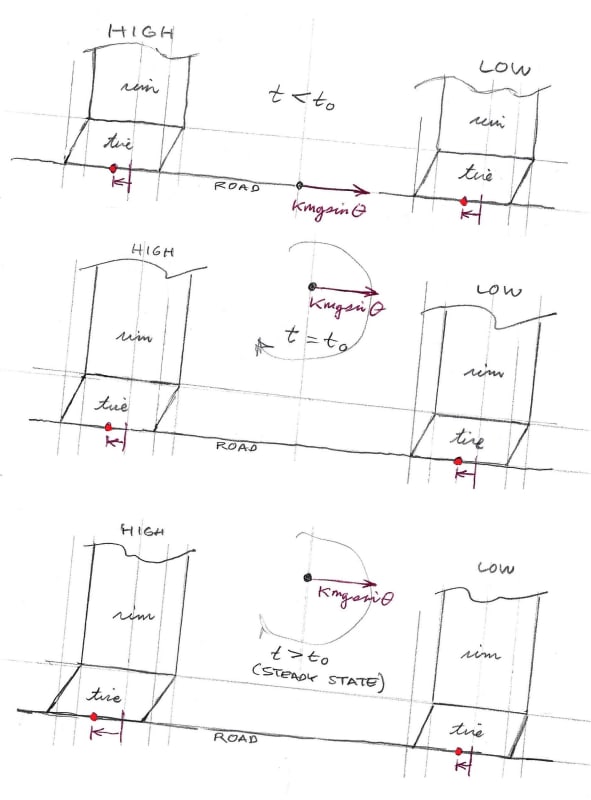
So in summary, the tire slip angles go from initial divergence (toe-out) in the transient state to parallelism (zero toe) in the steady state. Looking at Fy for each tire contact patch, the equalizing factor arises from tire deformation. It's simply an inevitable consequence of the differing tire velocities. As the initial paths diverge and the tire deformations grow, the deformations create equal and opposite internal forces (for the axle, that is,) that likewise grow, until the sum of the internal and external forces acting on each contact patch equalizes. When this sum equalizes, the slip angles become the same for both tires and the pneumatic trails become equal.
So there are three things influencing tire shape happening here. The first is the axle overturning Mx moment as you call it, which somewhat compresses the lower tire's sidewall and slightly extends the higher tire's sidewall. Then we have the kmgsin(theta) force exerted on the axle arising from the rear axle's burden of the vehicle's weight, creating negative camber for the higher tire and positive camber for the lower tire. And then finally we have this changing camber in the transient state arising from the divergent velocities causing the contact patches to spread a bit farther apart from each other. This camber contribution is negative for both tires.
On edit, here's a schematic sketch of what I believe is happening as time passes:
I hope I'm not needlessly repeating myself but hopefully, this clarifies my thought process; please feel free to shoot this theory full of holes as needed. That's why I came here!