BioMes
Bioengineer
- Nov 2, 2022
- 40
Hello everyone!
I’ve seen the following forum thread:
but I still have some doubts regarding this quality measure.
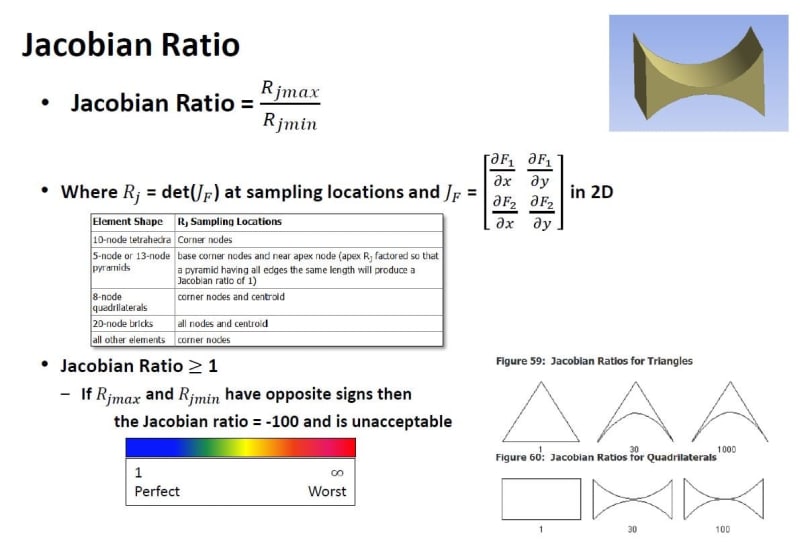
1) Most importantly, I can’t find a single universal definition. Even ranges seem to vary a lot depending on the software. Usually, the range is given as 0 to 1 with 1 being the perfect shape but, as we know, negative values are also possible and indicate inverted elements. So shouldn’t the range actually be -1 to 1 or does it depend on the software too? The aforementioned forum thread also gives two ranges. In some software (like SolidWorks Simulation) much higher positive values are possible. Is it really the case that Jacobian can be defined so differently? Shouldn’t this measure be more unified like aspect ratio?
2) My second doubt is about element types for which Jacobian makes sense as a quality measure. I know that it mostly applies to second-order triangles and terahedra but are all the other element types (like linear triangle and tet and linear/quadratic hex) also verified with this criterion? The linked thread mentions that linear triangle and tet elements always have a Jacobian value of 1 (so it can’t indicate their distortion) but is it really the case regardless of the definition? What about hex elements?
I’ve seen the following forum thread:
but I still have some doubts regarding this quality measure.
1) Most importantly, I can’t find a single universal definition. Even ranges seem to vary a lot depending on the software. Usually, the range is given as 0 to 1 with 1 being the perfect shape but, as we know, negative values are also possible and indicate inverted elements. So shouldn’t the range actually be -1 to 1 or does it depend on the software too? The aforementioned forum thread also gives two ranges. In some software (like SolidWorks Simulation) much higher positive values are possible. Is it really the case that Jacobian can be defined so differently? Shouldn’t this measure be more unified like aspect ratio?
2) My second doubt is about element types for which Jacobian makes sense as a quality measure. I know that it mostly applies to second-order triangles and terahedra but are all the other element types (like linear triangle and tet and linear/quadratic hex) also verified with this criterion? The linked thread mentions that linear triangle and tet elements always have a Jacobian value of 1 (so it can’t indicate their distortion) but is it really the case regardless of the definition? What about hex elements?