Hello,
I have a simple conceptual toy problem that I am trying to implement in Abaqus, but without success. Could someone please help me?
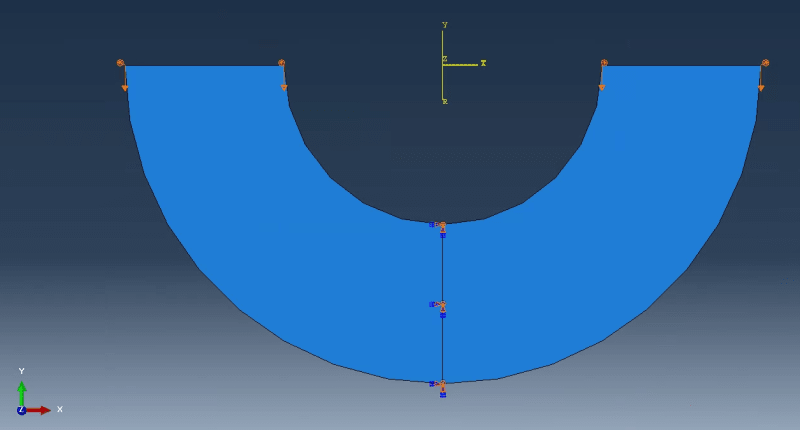
I have a cut sector of an annular sheet (see picture). Imagine it to be made of paper in real life. If I now bring the two edges (lying along the x-axis here) close to each other and attach them with some tape, the entire sheet will curve into a conical sector. How do I implement this problem in Abaqus? I have tried to do it with some BCs at the two edges, and with a Static, General step. But it's not working, and quits with errors.
Any ideas?
I have a simple conceptual toy problem that I am trying to implement in Abaqus, but without success. Could someone please help me?
I have a cut sector of an annular sheet (see picture). Imagine it to be made of paper in real life. If I now bring the two edges (lying along the x-axis here) close to each other and attach them with some tape, the entire sheet will curve into a conical sector. How do I implement this problem in Abaqus? I have tried to do it with some BCs at the two edges, and with a Static, General step. But it's not working, and quits with errors.
Any ideas?

