Yorik
Student
- Jun 21, 2023
- 4
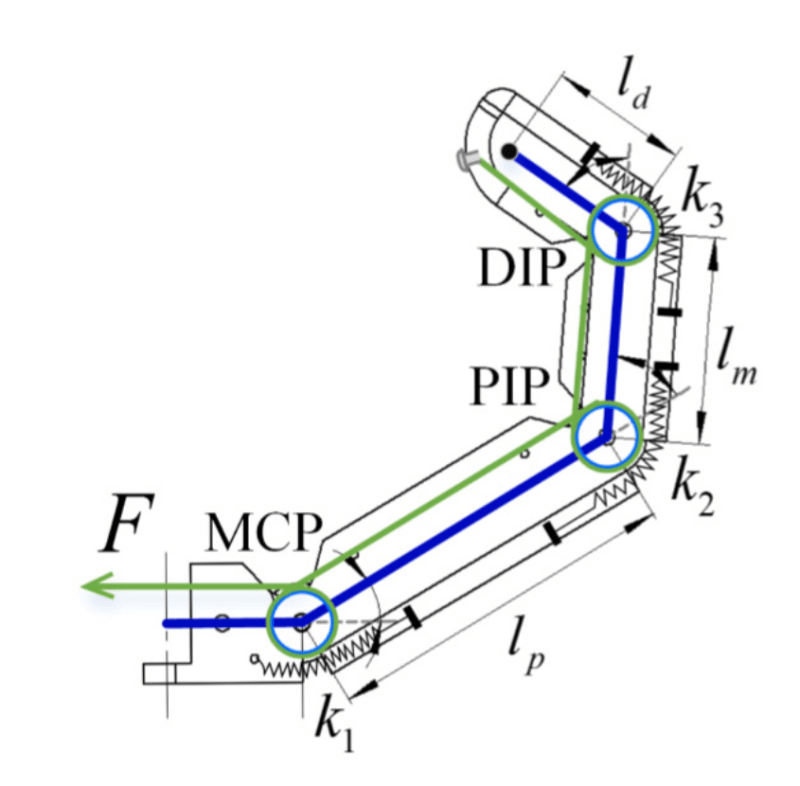
I am working on creating a robotic finger with the design choice as in the picture above. The green cable should be attached to a motor/pulley, which is the driving actuator. The cable is then wound around three passive joint pulleys in the finger and each joint has a counteracting spring for returning to its rest position. Before going to a real setup, I am modeling the dynamic equations of this system in Matlab. I derived dynamic equations using the Euler-Lagrange method on a triple pendulum, which of course does not yet include the cable mechanism. Now, I have equations for all three joint torques [tau1, tau2, tau3].
From here, I do not know how to model the cable transmission mechanism and relate the motor torque (tau_m) to the individual passive joint torques. It is obvious that in a kinematic chain like this, the first joint experiences a higher torque than the second and third due to gravity, inertia and external forces further on in the kinematic chain. However, since the joint are coupled through the cable and to the motor torque and the latter is the only variable I can control, how do the dynamic equations relate to the individual joint torques?
Because, in a cable (I know there are some losses due to friction, but leave them out for now) the tension force should be the same along its entire length. But if the tension is the same everywhere, then also should the induced torque in all joints, right? This seems like a contradiction to me.
Can someone try to explain what happens in a mechanism like this and how to model the dynamics properly?
