Oaklandishh
Mechanical
- Sep 3, 2014
- 48
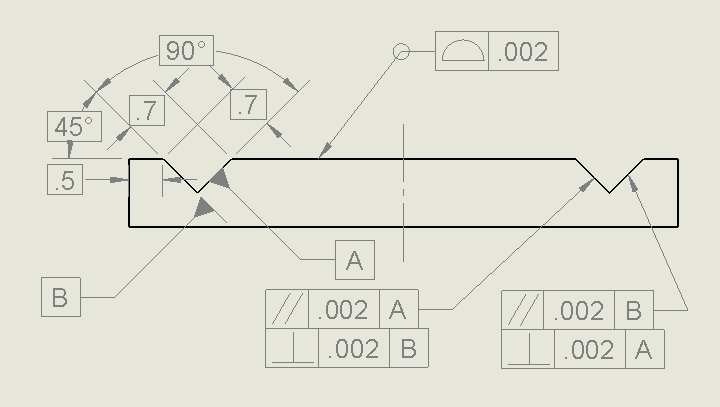
Assuming I have a double V block part as shown below, and the design intent is to keep the axis of the two imaginary cylinders lying in the part parallel and in the same plane, what is the best way to do this?

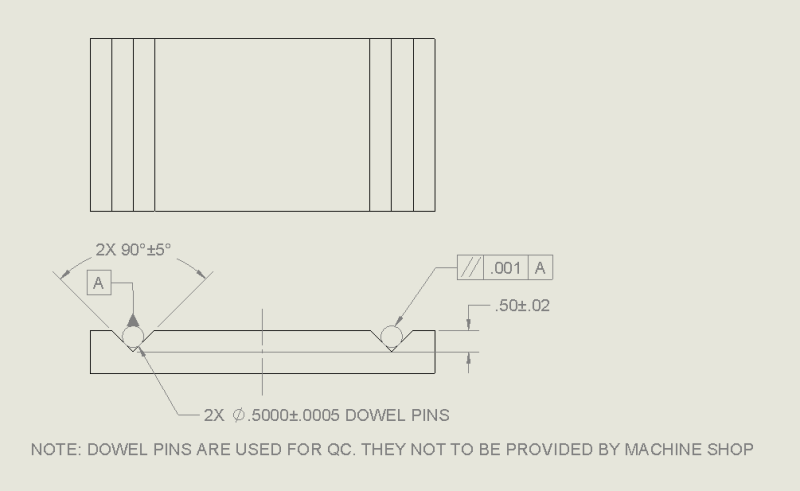
I have some ideas as to how to make this happen (below), but I am unsure as to how I would actually QC the parts in real life.
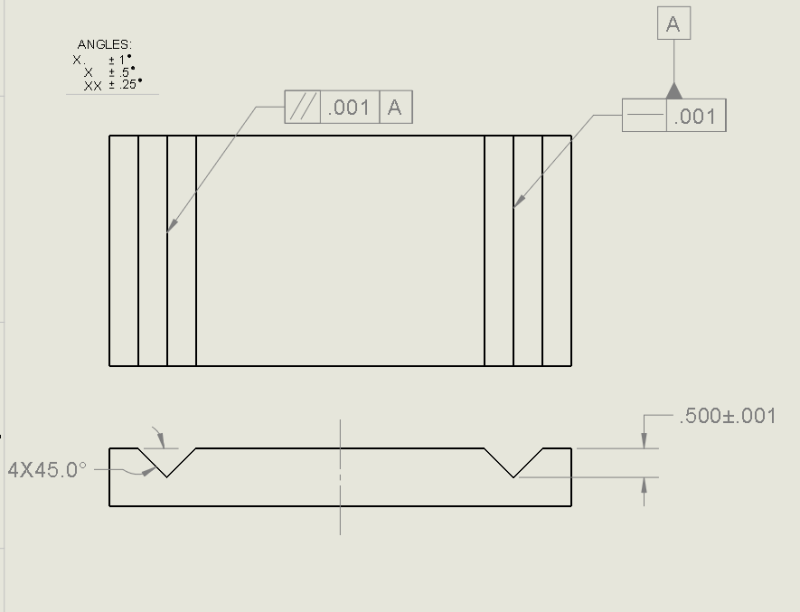

I have some ideas as to how to make this happen (below), but I am unsure as to how I would actually QC the parts in real life.