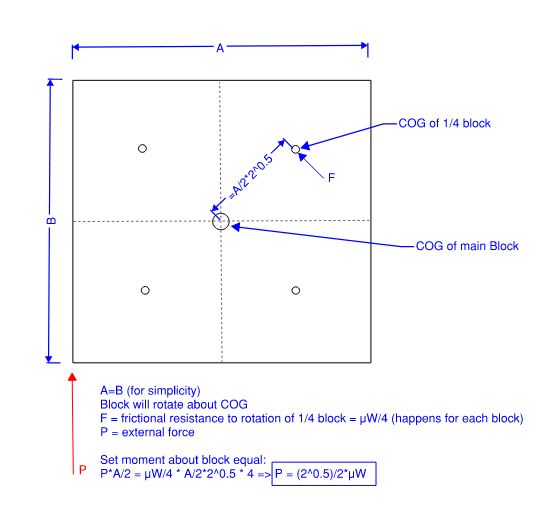
I'm having problems working out when a kentledge block with an eccentric force will slide.
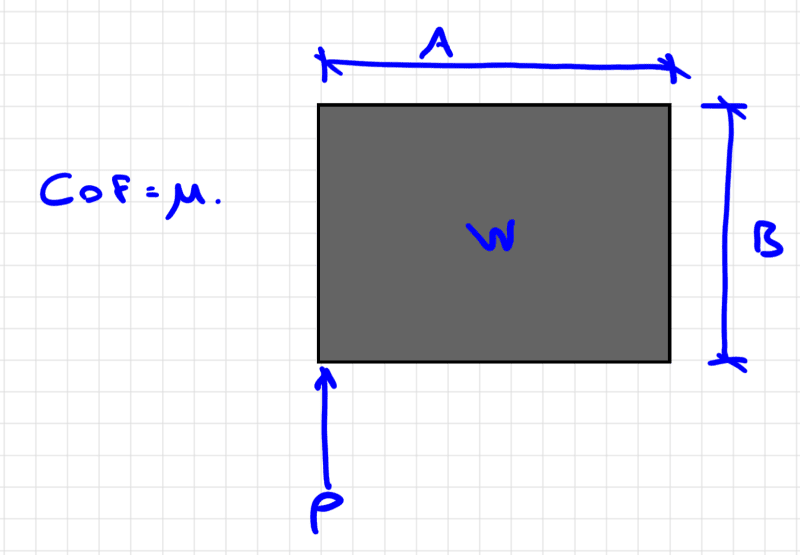
As per image below, say block has plan dimensions of A x B, a weight of W and the sliding force P is applied on the very edge of the block.
I've done a few circles in my thinking now and so far google hasn't yielded anything either!
Any input appreciated!
Martin.
As per image below, say block has plan dimensions of A x B, a weight of W and the sliding force P is applied on the very edge of the block.
I've done a few circles in my thinking now and so far google hasn't yielded anything either!
Any input appreciated!

Martin.