Lateral-Torsional Buckling AISC

[SoFloJoe]

I am working on a beam design that has dynamic loading for a trolly monorail design.

The structure already exists, the facility is upgrading their trolly crane system and I am analyzing this existing structure to make sure it can handle the new loads.

I have ran the loads and it all checks out, deflection is good, shear and moments are within limits per Florida Building Code and CMAA. But following AISC Steel Manual (14th ed) the Lateral-Torsional buckling is not working out for me. The verbiage is a bit confusing and was hoping that I can get some clarification here.

My process is as follows:
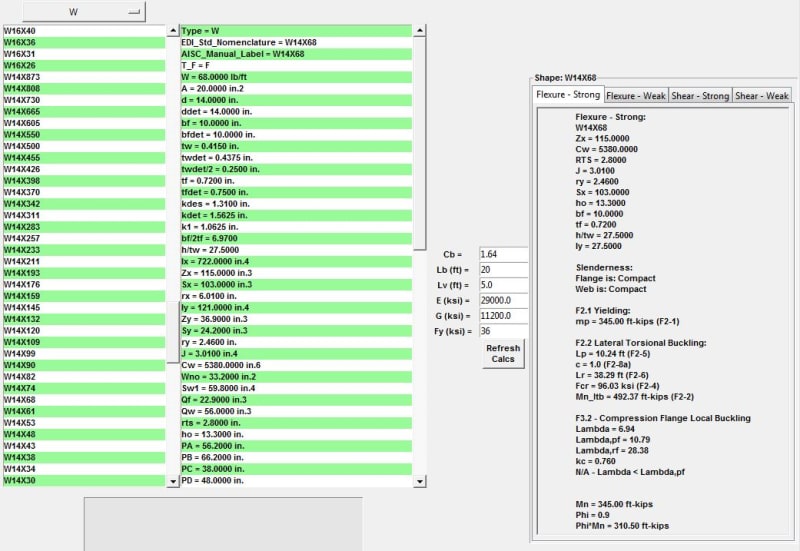
- It is an I-beam W14x68
- Per Table B4.1b Case 10 it is classified as a non-compact Flange
- Per F3, it states to follow F2.2 procedure. But what about F2.1?
- Cb = 1.64
- This is where it gets confusing, AISC states that Mn = Mp = FyZx and also states that Mn shall be the lower value obtained. But the equation F2-2 uses both of these variables. I am right now assuming that Mp = FyZx (F2.1) and Mn will be the result of equation F2-2. Though the result of F2-2 should be < or = to Mp. And it is not per my calculation. Is my assumption incorrect and have I reversed Mp and Mn? Am I even using the right Mp?
- I also looked up the member using table 3-10, my unbraced length is 20ft and available moment using LRFD is 310.5 ft-kip. This puts the W14x68 well within the limits.

I am not sure what to do. If the Lateral-Torsional Buckling is indeed outside the limits then the only option other than switching out the i-beam that I would think of would be to cut the span with additional support but this will not make the client happy, are there any other options?

Below are clips from my excel to better explain. Thanks in advance for your help!

 

[JoshPlumSE]

This is a compact flange (b/t) = 6.9 = bf / 2tf.... Did you forget to divide by 2?

Note:
The AISC manual adds a footnote to all the WF shapes in Table 1-1 which have slenderness issues at 50ksi.

 

[SoFloJoe]

Thanks JoshPlum.

From what I understood per AISC I am not at that point yet, divide by two in the next part (F3.2) I am still in F3.1 Lateral-Torsional Buckling which refers to F2.2. In order to classify the member I had to use Table B4.1 case 10 which refers to the width to thickness ratio but does not divide by 2.

I see the note you are referring to. Even if I consider it a compact flange and use section F2 instead of F3 I am still having issues with the F2.2 Lateral Torsional Buckling.

Thanks again for your help!

 

[Bobby46]

In B4.1 case 10, the dimension "b" is shown as half of the flange width(bf). So, b/t = (bf/2)/tf

 

[Bobby46]

Mp should always be Fy*Zx

You will calculate an Mn for each failure mode (i.e. F2.1, F2.2, etc)

It is very possible that your Mn for LTB is higher than your Mn for yielding. This will happen if your unbraced length (Lb) does not fall within the applicable range for an LTB failure. It is just how the algebra works out for (Lb-Lp)/(Lr-Lp). This just means that your beam will fail by yielding before LTB for the given loading

*Edit: Your Cb factor also effects the LTB calculation. LTB appears to control for your beam with Cb=1.00, but not Cb=1.64

 

[IFRs]

Your Excel is one of the best and clearest I've seen in a long time. Any chance you could post it?

 

[BridgeSmith]

Bobby46 is correct. LTB doesn't appear to be a critical failure mode for your beam. However, it is due to the combination of the unbraced length and the way it is loaded.

The loading pattern results in a fairly high Cb factor. If the loading was less varied within the same unbraced length, the Cb would be lower and LTB could control, since Lb > Lp. LTB could be critical under different loading conditions.

Edit: Just saw your edit, Bobby46, so this post just became mostly superfluous.

 

[Celt83]

looks like your using 36 ksi for W14x68, also your "NG" should really read "Yielding Controls - Mn = Mp"
here is what I get for 36 ksi and the same cb and Lb:

and at 50ksi:

Open Source Structural Applications:

https://github.com/buddyd16/Structural-Engineering

 

[SoFloJoe]

Thank you for all your inputs.

n B4.1 case 10, the dimension "b" is shown as half of the flange width(bf). So, b/t = (bf/2)/tf

Thanks I did not see the note (B4.1a) where it states to half it. I did this and found the member to be compact in the flange and web.

looks like your using 36 ksi for W14x68
here is what I get for 36 ksi and the same cb and Lb:

Thank you for confirming, yes I am assuming 36ksi staying conservative since it as an existing beam. BTW which software are you using? looks helpful, Is it the github link below?

So the value from eqn F2-2 is ok? even though it is greater then the Mp value? I see the note in AISC that states to use the smallest of the values so I should go with the Mp value, correct?
EDIT: I missed your comment that yielding controls instead of using NG. Thanks! I think that answers my question.

Your Excel is one of the best and clearest I've seen in a long time. Any chance you could post it?

Thanks IFRs! It is still a working spreadsheet, once complete I would love to share.

Thanks again everyone!

 

[Celt83]

@SoFloJoe:
yeah that is the steel_calculator.py file, it needs the three v15 csv files and the aisc_database_class.py in the same folder to run properly.
Link


Open Source Structural Applications:

https://github.com/buddyd16/Structural-Engineering

 

[BridgeSmith]

"So the value from eqn F2-2 is ok? even though it is greater then the Mp value?"

The resulting value from the complete eqn F2-2 is Mp (the right end of the equation is "≤ Mp"). Very often, especially with a high Cb value, the calculated value will exceed Mp.

 

[JLNJ]

I would add in a little horizontal load, especially if you are going to wring every bit of strength out of the section by setting Cb > 1.00.

 

[dik]

An SMath construct that works... this if for HSS so no w value.

It's an easy construct and can be modified for other b/t or h/w values.

Dik