Greenalleycat
Structural
Howdy all,
I do my beam moment-capacity calculations from a typical spreadsheet that bases the capacity off a concrete strain of 0.003 and uses the stress block stuff - the same as you all do no doubt.
This is all fine and dandy until you run into a situation like mine, where you have steel with a low tensile strain capacity that is actually significantly more limiting than that concrete strain
To put numbers to it, my steel has an allowable strain of 1.5% - running a typical beam design check with concrete strain at 0.003 gives a steel strain of 4.5%, 3x the limit
So, I've built a new spreadsheet that allows me to set an upper strain limit on the steel then back calculates the concrete strain etc from there
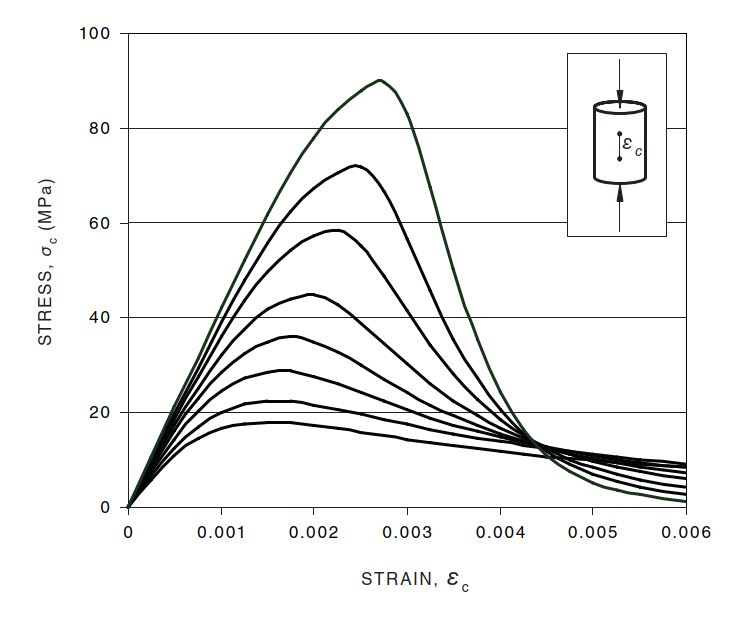
The problem is that I've had to make a fundamental assumption of a linear strain distribution through both the concrete and use this to calculate the concrete stress from stress = Young's Modulus * Strain relationship
I'm finding that I get concrete strains on the order of 0.001, or about 1/3 of the limit state strain, from this - is my assumption of linearity actually valid in this range?
I do my beam moment-capacity calculations from a typical spreadsheet that bases the capacity off a concrete strain of 0.003 and uses the stress block stuff - the same as you all do no doubt.
This is all fine and dandy until you run into a situation like mine, where you have steel with a low tensile strain capacity that is actually significantly more limiting than that concrete strain
To put numbers to it, my steel has an allowable strain of 1.5% - running a typical beam design check with concrete strain at 0.003 gives a steel strain of 4.5%, 3x the limit
So, I've built a new spreadsheet that allows me to set an upper strain limit on the steel then back calculates the concrete strain etc from there
The problem is that I've had to make a fundamental assumption of a linear strain distribution through both the concrete and use this to calculate the concrete stress from stress = Young's Modulus * Strain relationship
I'm finding that I get concrete strains on the order of 0.001, or about 1/3 of the limit state strain, from this - is my assumption of linearity actually valid in this range?