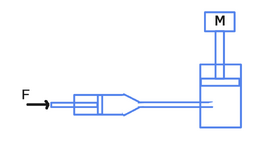
Good morning, I would like to ask you to model this problem, as I have some doubts. A constant force F acts on a hydraulic piston which is connected to a second piston that must lift a mass M. Inside the pipe, there is a constriction that causes a pressure drop. How can I write the differential equation that governs the motion of the piston lifting the mass M?
Navigation
Install the app
How to install the app on iOS
Follow along with the video below to see how to install our site as a web app on your home screen.
Note: This feature may not be available in some browsers.
More options
Style variation
-
Congratulations TugboatEng on being selected by the Eng-Tips community for having the most helpful posts in the forums last week. Way to Go!
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Mathematical Model Piston Pump 1
- Thread starter tomm0005
- Start date
- Status
- Not open for further replies.
goutam_freelance
Mechanical
Make a schematic of the system for clearer understanding.
- Thread starter
- #3
LittleInch
Petroleum
This is something that impacts speed of the lift and the maximum force available to lift the mass M
The pressure drop across the restriction will impact flowrate.
The pressure drop across the restriction will impact flowrate.
-
1
- #5
- Thread starter
- #6
thank you so muchI believe I may have come up with a solution as shown below, which appears to be a second order non-linear differential equation:
View attachment 874
LittleInch
Petroleum
Lets just go back to basics here.
Your mass M is just a vertical force which is M x g, so lets call it F1.
At rest / static, the pressure in the whole system is the same, so the equation F2 x A2 = F1 x A1
Now to get this mass to move upwards, you need to apply more force at F2, lets call it Fm.
The amount of Fm is variable depending on the velocity Vm of the Mass. This movement of the fluid creates a pressure drop in your constriction.
I think it should be easy to create an equation whereby movement of the F2piston creates a volumetric change, assuming this is a fixed F2 velocity, which results in a pressure increase in the F2 chamber. There will be an increase in the F1 chamber, but it is much lower and only really the piston friction so you can probably ignore it or add 10%.
So then solve fr different velocities of F2.
I still don't really know what is your variable that you are trying to find?
Your mass M is just a vertical force which is M x g, so lets call it F1.
At rest / static, the pressure in the whole system is the same, so the equation F2 x A2 = F1 x A1
Now to get this mass to move upwards, you need to apply more force at F2, lets call it Fm.
The amount of Fm is variable depending on the velocity Vm of the Mass. This movement of the fluid creates a pressure drop in your constriction.
I think it should be easy to create an equation whereby movement of the F2piston creates a volumetric change, assuming this is a fixed F2 velocity, which results in a pressure increase in the F2 chamber. There will be an increase in the F1 chamber, but it is much lower and only really the piston friction so you can probably ignore it or add 10%.
So then solve fr different velocities of F2.
I still don't really know what is your variable that you are trying to find?
Well I was close. I forgot to include the weight force of the mass acting down, and I did not realize that you can reduce the restriction effect to a linear function R*Q = R*A*V and then use an approximate value of R as shown. I think my equation is still correct if I include the Mg factor although it will be hard to solve as a non-linear equation with dx/dt to a power of 2.
Last edited:
BEMPE16524
Mechanical
yes considering you are using your brain while I'm just copy and paste from external resources, you are not wrong at all.Well I was close. I forgot to include the weight force of the mass acting down, and I did not realize that you can reduce the restriction effect to a linear function R*Q = R*A*V and then use an approximate value of R as shown. I think my equation is still correct if I include the Mg factor although it will be hard to solve as a non-linear equation with dx/dt to a power of 2.
BEMPE16524
Mechanical
I fully appreciate your talent. that's all.I did my analysis on my own without having tried to do a differential equation set up like this in about 20 years so I don't know what you are talking about.
Last edited:
goutam_freelance
Mechanical
- Thread starter
- #14
- Status
- Not open for further replies.
Similar threads
- Replies
- 10
- Views
- 3K
- Replies
- 9
- Views
- 3K
- Question
- Replies
- 5
- Views
- 6K
- Question
- Replies
- 5
- Views
- 4K
- Locked
- Question
- Replies
- 3
- Views
- 3K