Max pressure (bar) vs head (m) - centrifugal pump 1

[mladenf]

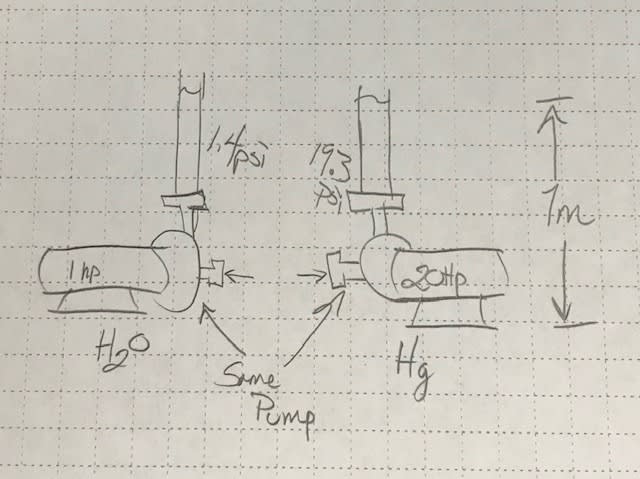
This was resume of one older thread:

"So bottom line, this pump is going to put out a certain head. And it will put out this same head regardless of the fluid. If the fluid is saltwater, the pressure will just be greater than if the fluid is gasoline - but the head will be the same. And on the flip side, if the pump requires 30 ft of head. That means it needs 30 ft regardless of fluid, even though saltwater would produce higher pressures than gasoline."

How can this be true? If one of the limiting factor for maximum head is energy input/electric motor, how can we have the same height of water and mercury for dedicated flow? Can someone provide indeapth explanation.

THX in advance

 

[Artisi]

Power input from the driver has nothing to do with generating the head and flow - - -
Required power input is a function, head, flow, and fluid density.

P = H x Q x SG / Eff.

It is a capital mistake to theorise before one has data. Insensibly one begins to twist facts to suit theories, instead of theories to suit facts. (Sherlock Holmes - A Scandal in Bohemia.)

 

[mladenf]

I don´t understand 1st statement. Isn´t it in collison with the 2nd one?
In equation you have SC, for mercury 15x greater then for water. What does that mean, that your EM and pump will deliver 15x power when run on mercury instead of water?

 

[Artisi]

mladenf, think the first statement was from another thread and was a conclusion to that thread - his second question is the one that needs an answer.

It is a capital mistake to theorise before one has data. Insensibly one begins to twist facts to suit theories, instead of theories to suit facts. (Sherlock Holmes - A Scandal in Bohemia.)

 

[mladenf]

Can anyone provide a reasonable explanation?

 

[JJPellin]

The pump requires the same amount of suction head regardless of the fluid. It would produce the same differential head regardless of the fluid. But, this says nothing about the driver. If you put mercury into the pump, the motor will almost certainly overload and trip off (or burn up) before it even gets up to speed. If you put a large enough driver on the pumps to drive it full of mercury, it would produce the same head. Now, that amount of pressure might exceed the maximum pressure rating of the casing or the mechanical seal. So, the case may spring a leak or the seal may blow out before it gets up to full speed. The original statement referenced was regarding hydraulic performance. There could be another constraint that makes it impossible to run a different fluid:

The coupling fails from over-torque.
The flange gaskets or head gasket blow out from over-pressure.
The driver overloads and trips from excessive horsepower.
The seal blows out from excessive pressure.

But, if you over-designed the coupling, driver, flanges and mechanical seal, the pump would produce the same head with any fluid.

Johnny Pellin

 

[3DDave]

For centrifugal pumps the amount of pressure output is proportional to the density of the fluid. Since the pressure from the fluid height is also proportional to the density, density cancels out.

At comparable speeds, the head will be the same no matter the density of the fluid, assuming viscosity is similar/negligible.

 

[mladenf]

OK, silly me. In my region we use the term flow for volume flow so this is a source of misunderstanding.
So we can have the same height for the same mass flow for 2 diff. fluids, but not for the same volume flow of those 2...
Didn't pay enough attention, THx everyone

 

[MortenA]

@mladennf, no. As JJPellin says above: If you overdesign everything you will get the same (volume) flow and head (lift height) no matter the desity. The PRESSURE will be different and the ENERGY consumption will be different though. So unless you overdesigned everything you would experience a lot of problems if you tried to pump mercury with a pump designed for liquid propane (as detalied above by JJPellin).

 

[LittleInch]

mladenf,

You've chosen an extreme range of SG to look at, but your final statement is not really true.

The issue is that there are a number of variables with a pump. When trying to compare different fluids then you can't go around changing other variables ( volume flow in this instance) without changing other things which impact on power like efficiency. If you look at the power curve of a pump it is not a flat line from zero at zero flow, so the energy required at a lower volumetric flow can easily be a higher amount per unit flow ( say kW per m3/hr)

From your OP you say "how can this be true?" Well it just is. Laws of physics etc.
If one of your limiting factors was the energy into a pump at a fixed speed then it becomes your limiting issue. If indeed you tried to change water for mercury at the same volumetric flow then the shaft power required would increase in the same ratio as the SG. You have though chosen a very extreme example. A more normal one would be something like swapping pumping gasoline for water.

Pumping higher SG products through a pump designed for one with a lower SG will cause an issue with power demand and you need to check the power of the motor to see if it is high enough to manage the new fluid at the same or similar volumetric flowrate. Sometime sit is, sometime it isn't.

Also the pressure will increase and again you need to check whether the new higher SG will cause you to exceed the class rating or design pressure of the pump casing or connecting pipes / flanges etc.

Remember - More details = better answers
Also: If you get a response it's polite to respond to it.

 

[mladenf]

Obviously I have a lack of knowledge.
So here is my modest opinion:

(1) P=m'*g*h= (2) V'*ro*g*h= (3) p*V' (without efficiency)

P power W
mass flow kg/s
g gravity m/s^2
h height m
V' volume flow m^3/s
ro density kg/m^3
p pressure Pa

Probably I overlooked something when interpreting the above equation:
(4) Mass flow is independent of the fluid pumped (the pump doesnt know the name of the fluid, so it pumps xy kg/s of every fluid on that specific height according to engaged power) but a volume flow is a function of density and therefore specific for every fluid. For m'1=m'2=const.; ro1<ro2 => V'1>V'2; and as a result, due to the determined power of the motor, p1<p2.

@JJPellin C/P:
"The pump requires the same amount of suction head regardless of the fluid. (5) It would produce the same differential head regardless of the fluid. But, this says nothing about the driver. If you put mercury into the pump, the motor will almost certainly overload and trip off (or burn up) before it even gets up to speed. If you put a large enough driver on the pumps to drive it full of mercury, it would produce the same head."

I know that you are right, but can you please give explanation concerning above paragraph, I am struggling You say: biger driver for mercury for the same head but that means that (1) -> P=m'*g*h, (4) and (5) is not true?

Thanks everybody for your patience (maybe if there is beginner's book or link to recomend linked with centrifugal pumps?)

 

[LittleInch]

If I read this right you've got mass and volume the wrong way around in item 4.

For the same volume flow the mass flow will vary as a proportion of density.

If you want to pump the same MASS flow then the power will stay similar providing that the efficiency isn't affected too much and you control the volume flow to match the mass flow change due to density
Centrifugal pumps are a variable volume, relatively constant (~20%) head machines.

You need to decide what is your constant (volume flow or mass flow) and what is going to vary. If you keep mass flow the same then the power required will be close, depending on efficiency of the pump.

Using mercury vs water is a bad way of looking at this as the difference is too extreme. It's like trying to compare lifting a 100kg weight vs a 10kg weight.
Use two fluids which are within 1.5 times each other in terms of density and then you won't get



Remember - More details = better answers
Also: If you get a response it's polite to respond to it.

 

[Rputvin]

I put a quick sketch on paper to highlight the difference. Same pump, same head, two very different motors for power needs, two very different pressures expressed in psi.