Mechanical Advantage 4

[bort72]

Hi All, I am learning about gears and I was hoping that you could help me with a question regarding mechanical advantage. I'm confused on 1 issue with 2 different examples -

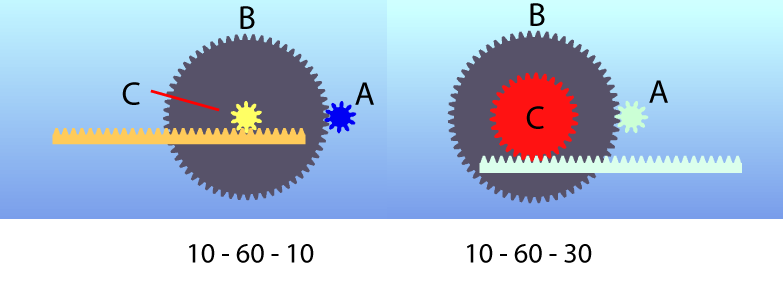
The "A" spur is the input gear, I'm trying to work out the torque that the "C" spur gear will have onto the rack. I understand that the bigger the PCD of the "C" spur, the faster the rack will move, but the relationship of "B" and "C" seems to be that of a class 2 lever where they are attached and share the same fulcrum, the load is in the middle "c" and the effort on the outside "b". So in the right version (10-60-30) would the mechanical advantage be 6:1 for the A-B gear X 2:1 for the B-C lever? 12?

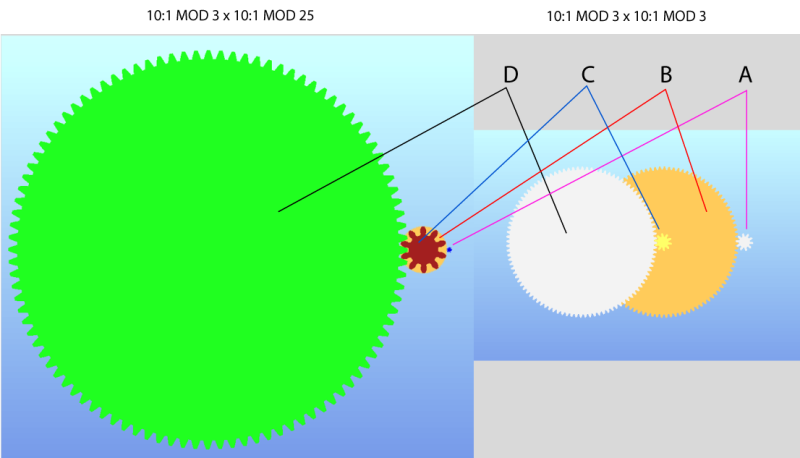
This image has the same 10:1x10:1 reduction in both versions, but on the left version the mod was changed. "A" is the input gear. I understand that both of these setups will have the same reduction in rpm. But the relationship between B and C looks like a class 2 lever.
My confusion started after reading this

https://en.wikipedia.org/wiki/Gear_train#Torque_ratio

which says that torque ratio = gear ratio = mechanical advantage.
So if both these setups have the same gear ratio and the relationship between B and C in each setup is vastly different, how can they have the same torque ratio?

So my question is - Can gears that are fixed to each other, on the same axis, be classified as a class 2 lever based on PCD and is that taken into consideration when calculating the mechanical advantage of a gear assembly? and if not taken into consideration, why not?

I appreciate your help, I want to understand the rules before I do the maths.
Thanks

 

[drawoh]

bort72,

A crude rule of thumb with simple spur gear trains is that the power in equals the power out. That means that the torque times the speed of gear[ ]A equals the torque times the speed of gear[ ]C. Try to work that out.

--
JHG

 

[gearcutter]

I understand that the bigger the PCD of the "C" spur, the faster the rack will move

This is not *really* correct.
Try to stop thinking of levers or pulleys when looking at gearing problems.
It's the number of teeth, not the radius length, that determines the torque ratio.

 

[3DDave]

The gears could be reduced to friction disks of the same diameter as the pitch diameter and the reduction/multiplication would be the same.

Conjoined gears can be analyzed as instantaneous class 2 levers. It is instantaneous because unlike levers the load is nominally perpendicular to the inputs and outputs, which is not typical for simple levers.

However, while lever theory is often used to introduced the action between gear teeth, higher level abstractions are usually easier to use, such as the ratios of tooth counts for complete gears. However, when getting back to a rack, with infinite teeth/infinite radius, the lever model is still useful.

 

[bort72]

Thanks so much for all your posts. I really appreciate the insight. 3DDave, are you able to suggest any reading, so that I can learn more about this. Thanks

 

[3DDave]

https://www.youtube.com/watch?v=A3X8cuJKyns

 

[bort72]

Thanks