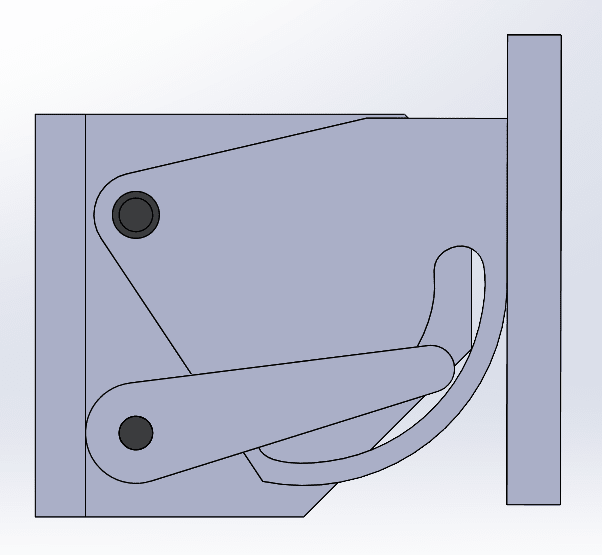
Hi everyone, I'm creating a mechanism to lift a weight and I need to make sure I'm calculating correctly in order to design the correct spring. The first image below shows you my current design, but I have realized that there is a lever action here that could drastically increase the force on my spring. In the moment diagrams I have outlined how I think I can mitigate the lever action by bringing. What I would like is for someone to correct my maths and basically show me what the force on the spring really is. Thanks
Current setup:
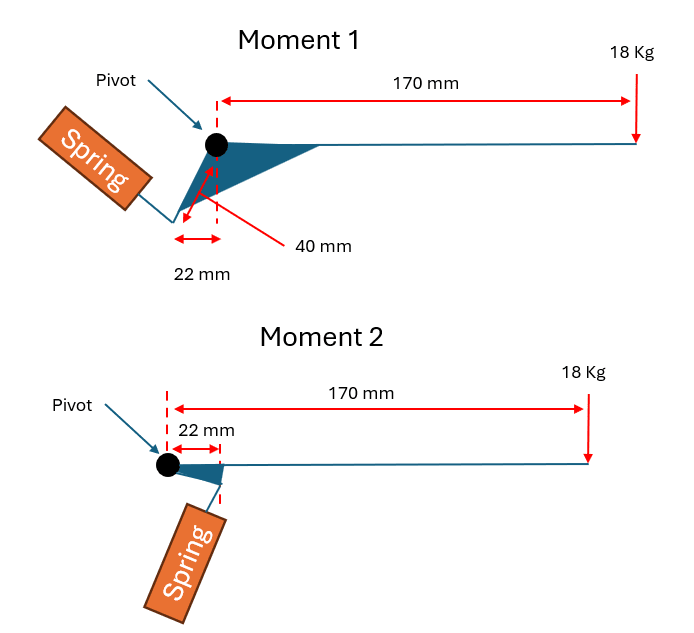
Force on spring: 18 x 9.81 x (0.170/0.040) = 750 N's
Potential Setup:
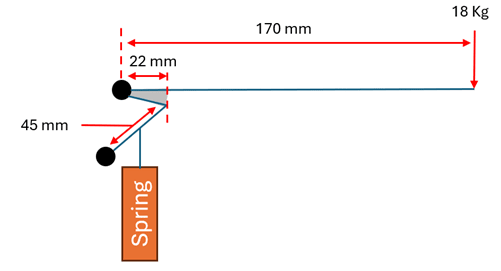
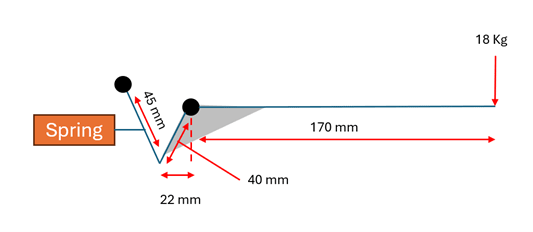
Force on spring: 18 x 9.81 x (0.17-0.022) = 26 N's
Current setup:


Force on spring: 18 x 9.81 x (0.170/0.040) = 750 N's
Potential Setup:

Force on spring: 18 x 9.81 x (0.17-0.022) = 26 N's